3.6.5 算例分析
选预测目标为输出层神经元，即工业、农业、生活及生态需水量作为神经元的输出层，以影响预测目标的特征因素作为输入层神经元，以历年各项统计资料为样本训练网络，其实质是寻找输入层神经元与输出层神经元间隐含的非线性映射关系，并据此预测有关目标。
在采用遗传神经网络模型进行需水量预测时，由于样本的数量及质量均对神经网络的训练有重要影响，考虑到黄河流域的资料来源及可靠性，本文选用1980～2000年共21年的历史资料，前18年用于训练样本，后3年用于网络拟合检验，因素序列见表3-14，需水序列见表3-15。
表3-14 黄河流域需水的影响因子值序列
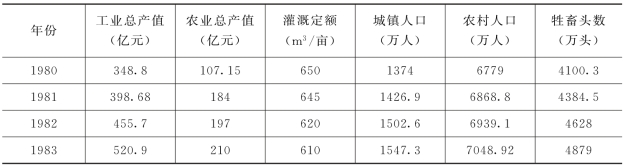
续表
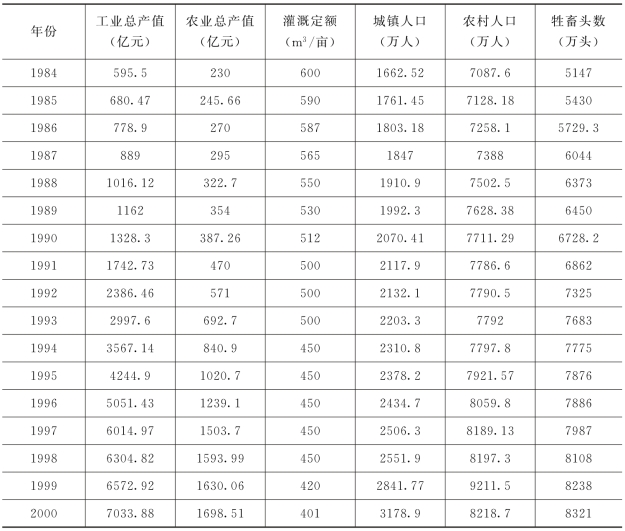
表3-15 黄河流域的历史需水序列 单位：亿m3
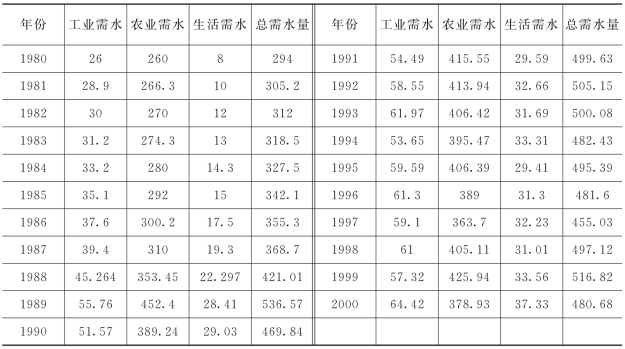
表3-16拟合结果显示，网络输出的数据误差的绝对值最小为0.88125%，最大为10.5007%，几乎全部介于0～10%，这说明训练精度较高，能够满足要求，所以可以进行网络的预测。从图3-6的拟合曲线可看出，实际输出与期望输出拟合较好。
表3-16 数据拟合结果
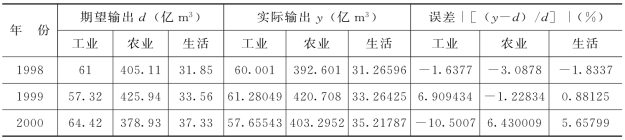
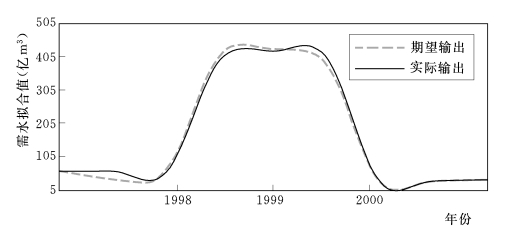
图3-6 期望输出与实际输出的拟合图
由于生态需水历史资料缺乏，生态需水量按《黄河的重大问题及其对策》（2000）提出的生态环境低限需水量处理，即在考虑水土保持因素影响、输沙水量、非汛期基流量以及下游蒸发渗漏4种因素，4个水平年的生态需水量均为210亿m3。所以模型输出层仅为工业、农业以及生活需水量3组量值。预测结果见表3-17，2010年、2020年、2030年需水量分别为577.6亿m3、630.28亿m3、663.17亿m3。
表3-17 工业、农业及生活需水预测结果 单位：亿m3
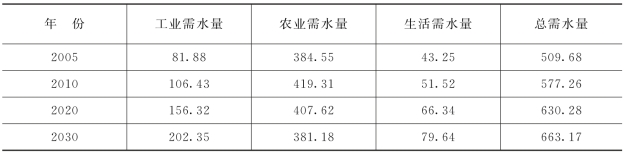
由于神经网络具有记忆、自联想功能，能通过历史样本的学习来搜集未来相关的信息，所以预测结果必然和已知的样本有一定的关联，并表现出一定的发展势态。预测结果基于两方面进行考虑：①从已有的历史资料中获取信息进行比较分析，这是由于神经网络的自学习、自联想能力所确定的；②从社会发展的角度进行比较分析。从表3-17可以看出，随着社会经济的发展，工业化水平及人民生活水平的提高，工业及生活需水均表现出增长的趋势，但农业需水在2010年后表现出递减的趋势。