11.3.2 主要风险因素筛选
在建立了风险影响因素集后,要从其中进一步筛选出主要风险因素,属深层次的风险识别。判断风险因素是否为主要风险因素的依据是各因素对预期目标影响程度大小。如果各风险因素与目标具有长系列同步资料,可采用传统数理统计方法——多元回归分析和主成分分析确定各风险因素对目标的影响程度。确定主要风险因素还可用灰色关联分析法和层次分析法。
11.3.2.1 多元回归分析模型
用多元回归分析模型辨识主要风险因素要分为两步,即整体相关性检验和各因素与目标的相关程度分析。整体相关性检验能说明所分析的多个风险因素对目标影响程度的高低,而各因素与目标的相关程度分析能识别每个因素对目标的影响大小。
设水资源系统中的某个目标y与m个风险因素x1,x2,…,xm均有n个同步统计资料(x11,x12,…,x1m,y1),(x21,x22,…,x2m,y2),(xn1,xn2,…,xnm,yn)。由概率统计原理得多元线性相关分析模型为:
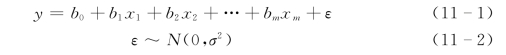
式中:b0,b1,b2,…,bm,σ2为与x1,x2,…,xm无关的未知参数。



11.3.2.2 主成分分析模型
主成分分析法是指标筛选最常用的方法之一,该方法的本质目的是要在力保数据信息丢失最小的原则下,对高维变量空间进行降维处理;经线性变换和舍弃一小部分信息,以少数的综合变量取代原始采用的多维变量。
设原变量为x1,x2,…,xJ,主成分析后得到的新变量为z1,z2,…,zm,均是x1,x2,…,xJ的线性组合(m<J)。变量z1,z2,…,zm构成的坐标系是在原坐标系经平移和正交旋转后得到的,称z1,z2,…,zm张成的空间为m维主超平面。在主超平面上,第一主分量z1对应于数据变异最大的方向V(z1),z2,z3,…,zm依次对应数据信息变异方向为V(z2),V(z3),…,V(zm),因此存在V(z1)≥V(z2)≥…≥V(zm),z1是携带原数据信息最多的一维变量,而m维主超平面是保留原始数据信息量最大的m维子空间。
主成分分析的步骤如下:


如果主因子载荷矩阵中某元素(或绝对值)比较大,说明对应的该因素是显著风险因素,否则,判定该因素不是主要风险因素。
11.3.2.3 灰色优势关联分析模型(https://www.daowen.com)


R中的每一行表示同一因素对不同目标的影响,每一列表示不同风险因素对同一目标的影响。起主要影响的因素称为优势因素,因此,有相应的优势因素与优势目标。如果某一行的各元素均大于其他行相应的元素,则该行相应的风险因素为优势因素,即对各目标影响都很大的因素,相对于所选目标而言,显然是主要风险因素;如某一列的各元素均大于其他列相应的元素,则该列相应的目标为优势目标,即各风险因素对其影响都大于对其他目标的影响,是进行风险分析应重点考虑的目标。如果R中的某个元素是所有元素中的最大者,则相应的因素对对应目标影响最大。
11.3.2.4 层次分析模型
经过初选的风险因素中,有些风险因素无统计资料或统计资料甚少,不便用相关分析模型,也不便用灰色优势关联分析模型。针对这些因素可采用层次分析模型来辨识主要风险因素。层次分析模型简称AHP模型,从本质上讲是一种思维方式,它把复杂问题分解成各个组成因素,又将这些因素按支配关系分组形成递阶层次结构,通过两两比较及计算矩阵最大特征根和特征向量,来确定各因素相对最高层排序权向量,再根据各因素相对目标的排序权值的大小,选择主要风险因素。排序权值越大,说明对目标的影响越大,因此选择其为主要风险因素。层次分析法模型整个过程体现了人的决策思维的基本特征,即分解、判断和综合。
层次分析模型分析问题时,通常按下述步骤进行,如图11-3所示。
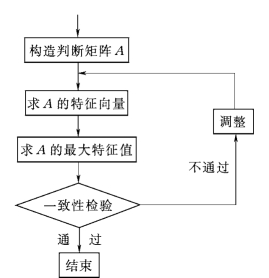
图11-3 层次分析模型流程图
(1)分析系统中各因素之间的关系,建立系统的递阶层次结构。
(2)对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较判断矩阵。
(3)由判断矩阵计算被比较元素对于该准则的相对权重。
(4)计算各层元素对系统目标的合成权重,并进行排序。
层次分析模型能将定性问题定量化,它对于解决大系统的多层次、多目标问题行之有效,具有高度逻辑性、灵活性及简洁性等特点。它的基本原理是将待评价的各因素两两比较相对重要性,然后进行排序;由于人判断的片面性,两两比较的结果不一定具有客观一致性,因此通常需要一致性检验。若不能通过检验,传统的做法是凭着大致的估计来调整判断矩阵,这样虽行之有效,但毕竟带有主观性和盲目性,有时需要经过多次调整方能通过一致性检验。为了提高模型求解效率,推荐采用改进的层次分析模型。
改进的层次分析模型先采用自调节方式建立比较矩阵,然后将其转化为一致性判断矩阵,不需要进行一致性检验,其有数学上证明,求解步骤如下:
设pi(i=1,2,…,m)是P层次上的m个元素;G是其上一层次的元素;A是P关于G的判断矩阵,C是最优传递矩阵。


