3.3.2 趋势外推法（确定型）
社会经济现象随着时间的推移发展变化，常常是遵循一定的规律。把历史数据的规律辨识出来，经过科学的计算和经济分析，最后用数学函数表达式近似地来描述这一发展过程，并假设在今后的相当一段时间内，该现象仍将以这个表达式所预测的趋势发展下去。预测者用这个表达式所推算出来的数据来预测未来的方法，就是趋势外推法。
1.趋势外推法经典的假设条件
趋势外推法是以预测的连续原理作为基本依据来预测的，但预测必须满足下面两个假设。
（1）要求社会现象产生和发展的因素具有稳定性，即一段时间内发展变化不大。
（2）要求社会现象的发展是一个渐变的过程，而不是跳跃式的突变，也就是说，趋势外推不能预测由于社会变更、战争和科技上的重大突破引起的社会现象的变化。
2.趋势外推法预测的基本步骤
（1）选择预测者感兴趣的预测变量。
（2）收集这一变量在前段尽可能长的时期中的数据，值得注意的是，时间越近的数据对未来的影响越大。
（3）根据数据的变化特征确定基本数学模型。
（4）计算模型的参数。
（5）根据曲线模型预测未来。
3.趋势外推法基本模型
（1）指数趋势模型：
或
或
它的相对变化率
；当b>0时，y→∞；当b<0时，y→0。b在不同的场合具有不同的含义，马尔萨斯在《人口原理》一书中利用指数模型预测世界人口的增长时，曾得出非常悲观的结论，这皆因不加限制地外推所致。但是，这个模型在某一时期内（例如，当b>0且
时），描述包括人口增长在内的许多客观现象（诸如国民经济生产总值的增长、技术扩散或技术替代的早期发展阶段等）还是合理的，目前的工业需水预测多采用此方法。
（2）对数趋势模型：
或
其特点是，变化率随时间的推移而趋向于零。
（3）多项式趋势模型：
或
当m=1，2时，上述模型即为熟知的线性（直线）模型和抛物线模型：
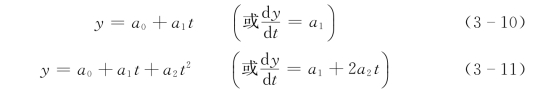
线性趋势的特点是变化率为常数，当a1>0时，y按固定比例增长；反之，按固定比例下降。当a2>0时曲线向下凸，当a2<0时曲线向上凸。仅就拟合（描述历史数据）而言，采用高阶多项式也许更好，但当用于外推（预测）时，人们很少用到3次以上的多项式。
（4）Logistic（逻辑期谛克）模型：
或
在上式中，l称为极限容量（在生态学中）或饱和水平（在描述技术扩散时）。这一模型最初是由比利时数学家、生物学家P.FVehulst在研究人口增殖规律时于1938年提出来的，至今仍有广泛的应用。
趋势外推法在系统比较稳定的情况下可单独应用。随着预测长度的增加，预测值的可靠性降低。需水预测中，由于需水的增长速度一般根据近期的增长趋势给出估计，因而对于长期预测，累计误差将增大。
4.算例
已知黄河流域1971～1980年的需水资料（表3-2）预测1981年的需水量。
表3-2 黄河流域1971～1980年的需水资料 单位：亿m3
（1）根据1971～1980年的流域需水资料，计算可知，环比系数在1.0附近，可采用指数趋势模型y=aebt进行计算。
其中可推得
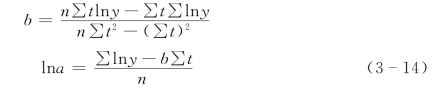
（2）计算系数a，b。计算参数见表3-3。
表3-3 计算参数
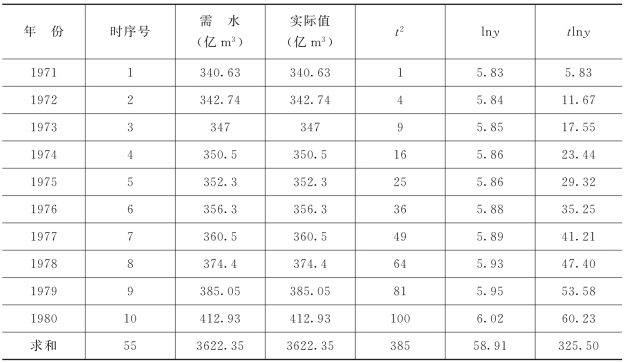
可以求知：
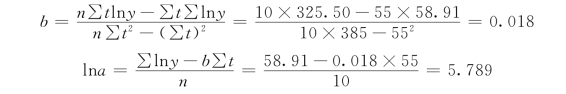
则a=eina=e5.789=326.97，b=0.018。
（3）预测计算。
建立指数曲线模型：
y=326.97×e0.018t
代入计算可得，1981年的水资源需求预测值：
y=326.97×e0.018t=326.79×e0.018×11=399.97（亿m3）
预测值与实际用水值415.2相比少了3.67%，误差尚能满足要求，分析原数据发现1980年的用水值较以前数列发生了一个小的突变，否则精度会更好。该法适合于需水时间数列较为平缓，即需水量值变动幅度不大的短期预测。