3.7.1 支持向量机理论
支持向量机SVM(SupportVectorMachine)是在统计学习理论基础上发展起来的,基于1909年Mercer核定理的一种新的机器学习方法。支持向量机又称为支持向量网络,具有理论完备、适应性强、全局优化、训练时间短、泛化性能好等优点,已经成为目前国际、国内研究的热点。支持向量机的核心内容是1992年才开始提出,到目前为止它是统计学习理论最成功的实现,且仍处于不断发展阶段。
SVM方法是从线性可分情况下的最优分类面提出的。所谓最优分类面,就是这样的分类超平面,它不但能够将所有训练样本正确分类,而且使训练样本中离分类面最近的点到分类面的距离(定义为间隔)最大。通过使间隔最大化来控制分类器的复杂度,进而实现较好的推广能力。在线性不可分的情况下,有所谓的广义最优分类面问题,即在追求最大化分类间隔的同时最小化错分样本的数目。
SVM是从线性可分情况下的最优分类面发展而来的。设给定训练样本集{(x1,y1),(x2,y2),…,(xl,yl)},其中xi∈Rd,i=1,…,l。此样本集是l个d维向量,yi∈{1,-1}或yi∈{1,2,…,k}或yi∈R,i=1,…,l。通过训练学习寻求模式f(x),使得不但对于训练样本集满足yi=f(xi),而且对于预测数据集{xl+1,xl+2,…,xm}同样能得到满意的对应预测值yi。模式f(x)称为支持向量机。当yi∈{1,-1}时为最简单的两类分类,yi∈{1,2,…,k}时为k类分类,yi∈R时为函数估计,即回归分析。
对给定训练样本集,假如训练样本集是线性可分的,则机器学习的结果是一个超平面,二维情况下是直线或称为判别函数,该超平面可以将训练样本分为正负两类。
若超平面wx+b能将训练样本分开,则有:
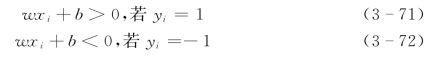
适当调整w和b,可将式(3-71)、式(3-72)改写成:
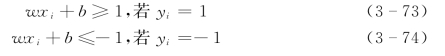
或者
![]()
根据统计学习理论,最优界面不但能将两类样本正确分开,而且能使分类间隔最大。如图3-7所示,实心点和空心点代表两类样本,H为分界面,H1和H2分别为各类样本中距分界面最近的样本且平行于分界面的面,它们之间的距离称为分类间隔。
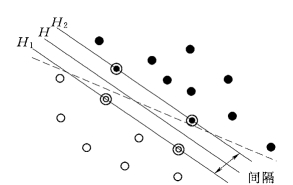
图3-7 线性可分情况下的最优分界面
所谓最优分类面就是要求分类面不但能将两类样本正确分开(训练错误率为0),而且使分类间隔最大。虽然图中虚线也能将两类样本分开,但它的分类间隔比H小。
分界面wx+b的分类间隔为:
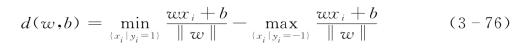
由式(3-75)、式(3-76)可得:
![]()
这样,最大化分类间隔d(w,b)问题就转化为在约束条件式(3-76)下最小化‖w‖2/2。由Lagrange乘子法,问题等价于在约束条件(https://www.daowen.com)

下最小化
![]()
每个Lagrange乘子αi对应一个训练样本xi。对应的αi>0的训练样本称为“支持向量”。最后得到的分类函数为:
![]()
式中:q为支持向量的个数。
如果训练样本线性不可分,上述的优化问题将变得无解。对于非线性分类问题,理论上应将输入空间通过某种非线性映射,映射到一个高维特征空间,在这个空间中存在线性的分类规则,可以构造线性的最优分类超平面。
由前面论述应知,线性的SVM是以样本间的欧氏距离大小为依据来决定划分结构的。非线性的SVM中以卷积核函数代替内积后,相当于定义了一种广义的距离,以这种广义距离作为划分依据。并不一定所有的学习机器都要以样本间距离作为划分依据,但是对于很多问题来说,把距离近的样本划分在一起确实是可行的。(可以想见距离近的样本会有更多的共同特征)
在上面的问题中只涉及训练样本之间的内积运算,这样在高维空间实际上只需进行内积运算,可以用原空间中的函数实现,甚至没有必要知道变换的形式。根据泛函的有关理论,只要一种核函数满足Mercer条件,它就代替某一变换空间中的内积。因此,在最优分类面中采用适当的内积函数K(xi,xj)就可以实现某一非线性变换后的线性分类,可实现非线性SVM,而这里并不需要直接进行非线性变换,计算复杂度没有增加。
核函数存在性定理表明:给定一个训练样本集,就一定存在一个相应的函数,训练样本通过该函数映射到高维特征空间的相是线性可分的,对一个特定的核函数,给定的样本集中的任意一个样本都可能成为一个支持向量。这意味着在一个支持向量机下观察到的特征在其他支持向量机下其他核函数并不能保持。因此,对解决具体问题来说,选择合适的核函数是很重要的。常见的满足Mercer条件的核函数有以下几种。
(1)多项式核函数:
![]()
(2)高斯径向基函数:
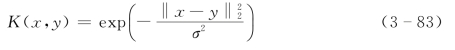
(3)Sigmoid函数:
![]()
此时的分类函数为:
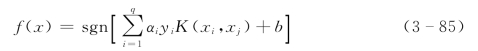
这就是支持向量机,其基本思想概括起来就是通过非线性变换将输入空间变换到一个高维乃至于无穷维的特征空间,使在特征空间中可以通过核函数展开定理来解决输入空间中的高度非线性分类和回归等问题。
