11.5.1 单目标风险决策
单目标风险决策方法有：最大期望效益值决策（EMV决策），乐观决策，悲观决策，折中原则决策，最大概率前景决策，贝叶斯决策和序列决策等。
11.5.1.1 最大期望效益值决策（EMV决策）
假定要在m个方案Ai（i=1，2，…，m）中选择决策一个最优方案，且每一个方案都有n个可能的结局Rj（j=1，2，…，n），如果已知采用方案Ai，结局为Rj时经济效果价值为μ（Ai，Rj）=μij，这里μ=μ（A，R）称为效用函数（1≤i≤m，1≤j≤n）。再假定每个方案选择后，可能出现的n个结局Rj（1≤j≤n）的发生概率P（Rj）=Rj为已知，而且满足P1+P2+…+Pn=1，则每一个方案Ai（i=1，2，…，m）的期望效用：
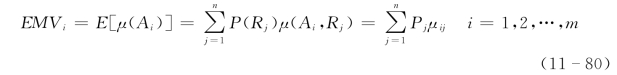
则最优方案A*满足：
由此可见，风险型决策的最优方案A*的满足条件是期望效益值最大。
11.5.1.2 乐观原则
乐观原则认为，哪个方案的前景点优势就应先取哪种方案，即：
式中：θj为指标值j的发生概率；l（Ai，θj）为方案i与指标值j的组合状态。
11.5.1.3 悲观原则
悲观原则称为最小最大原则，或称保守原则。决策者为了保险起见，要研究每一方案下所产生的最不利结果，再在这些不利结果中找出最好方案，用公式表示为：
11.5.1.4 折中原则
折中原则介于悲观原则和乐观原则之间，即对待决策的效果既不乐观，也不悲观，而是按折中决策。
式中：α为乐观系数，α∈[0，1]。
11.5.1.5 最大概率前景原则
最大概率前景原则认为，应按前景状态中概率最大并且有利结果选择。
11.5.1.6 贝叶斯风险决策
风险性决策所用的基本原理是贝叶斯（Bayes）定理，贝叶斯定理在前面已经给出，此处从略。
11.5.1.7 序列决策
序列决策的特点是各种方案及可能结果不是一个层次的简单决策，而是具有多个层次，能够分支的多级决策，可以用一个树形图来表示，故又称为决策树。
决策树方法解决序列问题十分有效，而且比较直观，便于决策人有顺序、有步骤地进行，也便于多层次的集体决策。通常这种决策方法与最大期望效益值方法给合起来使用。