5.1.5 水库优化调度的蚁群算法和粒子群算法
5.1.5.1 蚁群优化算法（Ant Colony Optimization）
1.算法原理
蚁群算法（Ant Colony Optimization，ACO）也称蚂蚁算法，是20世纪90年代初由意大利学者M.Dorigo提出的，它是根据蚂蚁觅食原理而设计的一种群体智能算法。在解决旅行商问题TSP（Traveling Salesman Problem）、二次分配问题QAP（Quadratic Assignment Problem）、车间调度问题JSP（Job-Shop Scheduling Problem）、车辆路线问题VRP（Vehicle Routing Problem）等组合优化问题时取得了一系列较好的实验结果。到目前为止，蚁群算法在水资源中应用的实例还比较少：Abbaspour等（2001）应用蚁群算法来估算非饱和土的水力参数；Maier等（2003）用蚁群算法获得了配水系统的近似全局最优解，并指出了蚁群算法能代替遗传算法用于配水系统的优化设计。
生物学研究表明，一群互相协作的蚂蚁能够找到食物源和巢穴之间的最短路径，而单只蚂蚁则不能。生物学家经过大量细致观察研究发现，蚂蚁个体之间是通过一种称之为信息素（pheromone）的物质进行信息传递的。蚂蚁在运动过程中，能够在它所经过的路径上留下该种物质，而且蚂蚁在运动过程中能够感知这种物质，一条路上的信息素踪迹越浓，其他蚂蚁将以越高的概率跟随此路径，从而该路径上的信息素踪迹会被加强，因此由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。蚂蚁个体之间就是通过这种间接的通信机制达到协同搜索食物最短路径的目的。
如图5-4所示，蚂蚁能够不使用可见的线索发现从食物源到巢穴的最短路径，而且它们能够适应环境的改变，一旦出现新的障碍物，旧的最短路径不再可行，那么就要寻找新的最短路径。图5-4（a）中蚂蚁正在连接食物源和巢穴的最短路径上移动，为了形成和保持这种路径所使用的主要方法是信息素轨迹。蚂蚁在行走期间投下一定量的信息素，当突然出现意想不到的障碍物阻断了初始路径后，它们会将被破坏的路径重新连接并发现最短路径，如图5-4（b）所示。那些刚好在障碍物前的蚂蚁不能继续跟踪信息素轨迹，不得不选择向右或是向左移动，如图5-4（c）所示。那些选择了障碍物附近较短路径的蚂蚁与选择较长路径的蚂蚁相比，将会更快地重新组成被阻断的信息轨迹。因此，在单位时间内较短的路径会接收到数量较多的信息素，这将引起更多数量的蚂蚁选择这条较短的路径。由于这个正反馈（positive feedback）过程，很快所有蚂蚁将选择这条较短的路径，如图5-4（d）所示。
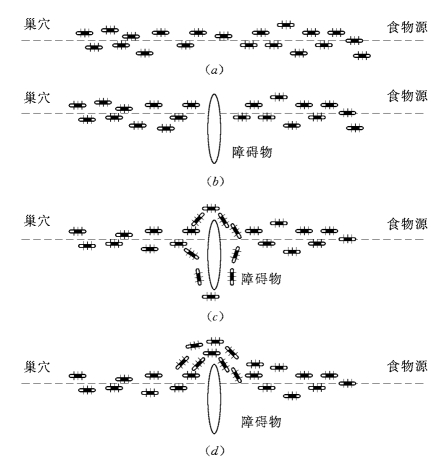
图5-4 蚁群觅食行为示意图
由此可以看出蚂蚁觅食协作方式的本质是：①信息素轨迹越浓的路径，被选中的概率越大，即路径概率选择机制；②路径越短，在上面的信息素轨迹增长得越快，即信息素更新机制；③蚂蚁之间通过信息素进行通信，即协同工作机制。
2.基本蚁群算法
蚁群算法是根据蚂蚁觅食原理设计的一种优化算法，在解决组合优化问题中表现出良好的性能。这里以TSP为例说明简单蚁群算法。
初始时刻，各条路径上的信息素量相等，设从城市i到城市j路径上的信息素轨迹强度τij（0）=C（C为常数）。蚂蚁k（k=1，2，…，m）在运动过程中根据各条路径上的信息素量决定转移方向。蚂蚁系统所使用的状态转移规则被称为随机比例规则，它给出了位于城市i的蚂蚁k选择移动到城市j的概率。在t时刻，蚂蚁k在城市i选择城市j的转移概率
为：
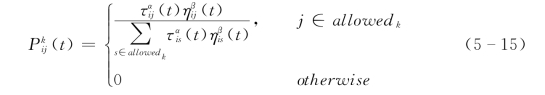
式中：allowedk={0，1，…，n-1}为蚂蚁k下一步允许选择的城市；τij为边（i，j）上的信息素轨迹强度；ηij为边（i，j）的启发式因子，反映由城市i转移到城市j的启发程度，这个量在蚂蚁系统的运行中不改变；
为蚂蚁k的转移概率；j为尚未访问的城市；α、β为两个参数，分别反映了蚂蚁在运动过程中所积累的信息和启发信息在蚂蚁选择路径中的相对重要性。
经过n个时刻，蚂蚁完成一次循环，各路径上信息素量根据下式调整：
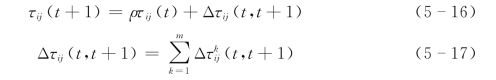
式中：
为第k只蚂蚁在时刻（t，t+1）留在路径（i，j）上的信息素量，其值视蚂蚁表现的优劣程度而定，路径越短，信息素释放的就越多；
为本次循环中路径（i，j）的信息素量的增量；ρ为信息素轨迹的衰减系数，通常设置系数ρ<1来避免路径上轨迹量的无限累加。
根据具体算法的不同，
的表达形式不同。M.Dorigo曾给出3种不同模型，分别称为蚁量系统（ant-quantity system）、蚁密系统（ant-density system）、蚁周系统（ant-cycle system）。在前两种系统中，蚂蚁在建立方案的同时释放信息素，利用的是局部信息；而蚁周系统是在蚂蚁已经建立了完整的轨迹后再释放信息素，利用的是整体信息。
基本蚁群算法流程如下。
（1）初始化A（t）（初始化蚁群）。
（2）评价A（t）（根据目标函数对每只蚂蚁的适应度作评价）。
（3）释放信息素（根据适应度，对蚂蚁所经过的路径按一定的比例释放信息素。适应度越高，所释放的信息素越多）。
（4）蚂蚁移动（蚂蚁依据前面蚂蚁所留下的信息素和自己的判断选择路径）。
（5）信息素的挥发（信息素会随着时间不断消散）。
3.改进蚁群算法
（1）蚁群系统ACS（Ant Colony System）。蚂蚁系统AS（Ant System）是ACO的最早形式，此后陆续出现了多种改进蚁群算法，如带精英策略的蚂蚁系统（Ant System-with elitist strategy，ASelite），基于优化排序蚂蚁系统（Rank-Based Version of Ant System，ASrank），蚁群系统（Ant Colony System，ACS），最大—最小蚂蚁系统（Max-Min Ant System，MMAS）以及最优—最差蚂蚁系统（Best-Worst Ant System，BWAS）。其中蚁群系统ACS将蚁密系统、蚁量系统的局部更新和蚁周系统的全局更新结合起来，在蚂蚁系统的基础上做了3方面的改进。
1）状态转移规则不同于蚂蚁系统中完全依概率选择路径的随机比例规则，引入了调整参数
，用以调节探索新路径的程度和是否使蚂蚁的搜索活动集中于最优解的空间领域内，称为伪随机比例规则。
按照上述方法可获得初始种群，且该初始种群必满足水量平衡方程，以及有关的上下限约束。这就使得初始种群中的每一个个体都是等式约束的可行解，可加速算法收敛。
4.ACS在水库优化调度中的应用
应用蚁群算法求解特殊问题，包括以下几个步骤：①将问题表述为类似于蚁群结构的图表形式；②在各时段指定启发式因子生成解（如被蚁群选择的路径）；③定义用于优化的适应度函数；④选择一种ACO算法应用于所研究的问题。在以下的介绍中，应用ACS算法解决水库（群）优化调度问题。
（1）以供水为目标的水库优化调度。
1）将水库优化调度问题概化为蚁群结构。水库（群）优化调度作为一种组合优化问题可以应用蚁群算法进行求解。求解时要考虑一系列入流，并将各水库库容离散成若干等份，根据优化准则决定各时段出库流量。连接不同时段的始、末库容可形成代表水库调度系统的若干条调度线，问题的一个解是各水库调度线的组合，这时即可决定各库出库。如图5-5所示。
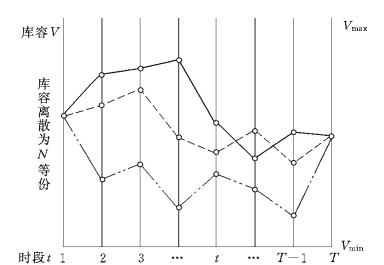
图5-5 水库优化调度的蚁群结构图
5.1.5.2 粒子群优化算法（Particle Swarm Optimization）
粒子群优化（Particle Swarm-Optimization，PSO）算法是1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出的，他们在当年的IEEE国际神经网络学术会议上正式发表了题为“Particle Swarm Optimization”的文章，标志着粒子群算法的诞生。其基本思想是受他们早期对鸟类群体行为研究结果的启发，并利用了生物学家Frank-Heppner的生物群体模型。
粒子群算法与其他进化类算法相类似，也采用“群体”与“进化”的概念，同样是根据个体（粒子）的适应值（fitnessvalue）大小进行操作。所不同的是，PSO算法的进化过程是一个自适应过程，粒子的位置代表被优化问题在搜索空间中的潜在解；粒子在空间中以一定的速度飞行，这个速度根据它本身的飞行经验以及同伴的飞行经验进行调整，决定它们飞翔的方向和距离。粒子们追随当前的最优粒子在解空间中搜索。PSO初始化为一群随机粒子（随机解），然后通过迭代来找到最优解。在每一次迭代中，粒子通过跟踪2个“极值”来更新自己，一个是个体极值，即粒子本身找到的最优解；另一个是全局极值，即整个种群目前找到的最优解。其中第i个粒子表示为一个N维的向量，Xi=（xi1，xi2，…，xin）为粒子i的当前位置；Vi=（vi1，vi2，…，vin）为粒子i的当前飞行速度；Pi=（pi1，pi2，…，pin）为粒子i所经历的最好位置，也就是粒子i所经历过的具有最好适应值的位置，称为个体最好位置，也可记为pbest；在群体中所有粒子经历过的最好位置的索引号用符号g表示，即pg=（pg1，pg2，…，pgn），也表示为gbest。
1.基本粒子群算法
有了以上定义，基本粒子群算法的进化方程可描述为：
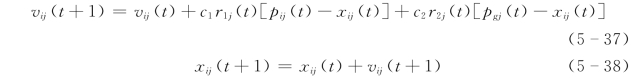
式中：j为粒子的第j维，j=1，2，…，N；i为粒子i，i=1，2，…，m；t为第t代；c1、c2为加速常数，通常在0～2间取值；r1、r2为0～1之间的随机数。
从上述粒子进化方程可以看出，c1调节粒子飞向自身最好位置方向的步长，c2调节粒子向全局最好位置飞行的步长。为了减少在进化过程中粒子离开搜索空间的可能性，vij通常限定于一定范围内，即vij∈[-vmax，vmax]。如果问题的搜索空间限定在[-xmax，xmax]内，则可设定vmax=k·xmax，0.1≤k≤1.0。
2.带惯性权重的改进粒子群算法
为了改善基本PSO算法的收敛性能，Shi Y.与Eberhart R.C.在1998年的IEEE国际进化计算学术会议上发表了题为“A Modified Particle Swarm Optimizer”的论文，首次在速度进化方程中引入惯性权重，即：
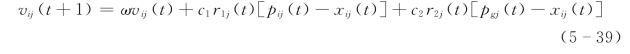
式中：ω称为惯性权重（inertiaweight）。
因此，基本PSO算法是惯性权重ω=1的特殊情况。惯性权重ω使粒子保持运动惯性，使其有扩展搜索空间的趋势，有能力探索新的区域。引入惯性权重ω可清除基本PSO算法对vmax的需要，因为ω本身具有维护全局和局部搜索能力平衡的作用。这样，当vmax增加时，可通过减少ω来达到平衡搜索；而ω的减少可使得所需的迭代次数变小。因此，可以将vmax，d固定为每维变量的变化范围，只对ω进行调节。式（5-38）、式（5-39）是标准的PSO算法，该算法需要用户确定的参数并不多，而且操作简单，使用比较方便。
式（5-39）中，第一部分是粒子先前的速度，第二部分为“认知”部分，表示粒子本身的“思考”；第三部分为“社会”部分，表示粒子间的信息共享与合作。在寻求一致的认知过程中，个体往往记住它们各自的信念，同时考虑同事们的信念，当个体察觉同事的信念较好时，它将进行适应性调整。
标准PSO算法流程如下。
（1）初始化一群粒子（群体规模为m），包括随机位置和速度。
（2）评价每个粒子的适应度。
（3）对每个粒子，将其当前适应值与其经历过的最好位置pbest做比较，如果好就将其替换成当前的最好位置pbest。
（4）对每个粒子，将其适应值与全局经历过的最好位置gbest做比较，如果好就重新设置gbest。
（5）根据式（5-37）、式（5-38）求变化粒子的速度和位置。
（6）如果未达到结束条件（通常为足够好的适应值或达到一个预设最大代数Gmax），则返回（2）。
PSO算法速度的改变由3部分组成：动量项、认知项和社会项。3部分如何平衡，决定了PSO算法的性能。标准PSO中增加了一个新参数为惯性权重，如前所述，它的引入是为了平衡全局搜索与局部搜索的能力。惯性权值较大，全局搜索能力强，局部搜索能力弱；反之，则局部搜索能力增强，而全局搜索能力减弱。有文献提出了基于模糊系统的惯性权重的动态调整，动态惯性权值可以在PSO搜索过程中线性变化，亦可根据PSO性能的某个测度而动态改变。随后，在Clerc的研究中，引入了另一个称之为收缩因子的系数，目的是确保算法收敛。从数学上分析，这两个参数是等效的。
3.改进PSO在水库优化调度中的应用
对水库优化调度问题而言，可假设一个N维的目标搜索空间，以年为调度周期时可取N=12，代表每年的12个月，粒子位置可代表水库水位。确定粒子种群规模为m，则第i个粒子在N维搜索空间中的位置是Zij，其中（i=1，2，…，m），（j=1，2，…，N）包含着一年中12个月的水库水位变化情况，则每个粒子的位置就是一个潜在解。第i个粒子最佳适应值所对应的解即为个体最优解pbest，整体粒子群在历代搜索过程中最佳适应值所对应的解为全局最优解gbest。
粒子根据式（5-38）、式（5-39）来进行位置和速度的更新，结合水库优化调度问题可写成：
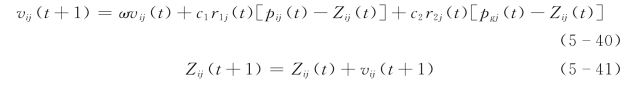
在水库优化调度中，最后输出的最优粒子值就是12个月的最佳水位变化值，而粒子适应度则代表模型选定的目标函数值。
根据标准PSO算法的基本理论，结合自适应粒子群算法进行自适应更新，求解水库优化调度问题的基本步骤如下。
（1）确定水库优化调度的目标函数，给定约束条件。
（2）确定粒子群规模m、空间维数N、最大迭代次数以及PSO算法基本参数c1、c2、r1、r2等。
（3）随机产生初始粒子，计算初始粒子的适应度，并挑选出最优粒子。
（4）利用更新公式对粒子进行位置和速度的更新迭代。初始粒子的第一次迭代，其个体最优就是其本身，随后则采用在解空间移动时所经历的最好点。在迭代过程中，如果计算出的速度超过了最大限速，则将其值设定为最大速度；如果粒子某一维的位置超过了初始粒子的生成空间，则取其极值代替。
（5）判断更新后的粒子是否满足约束条件，包括水量平衡方程、水位库容约束、出库流量限制等。如不满足，则抛弃该组粒子，重新随机生成一组粒子满足约束条件。
（6）判断水位连续变化情况，如变化较小，则进行自适应更新，避免早熟收敛。
（7）计算更新后粒子的适应度，比较选择，记录粒子的个体最优位置和全局最优位置。
（8）判断是否满足最大迭代次数，如满足退出循环，得到最优解；否则转向（4）。