8.4　黄河流域水资源多维临界调控程序

在特定时段，多维临界调控不可能涵盖所有的分目标，这样在进行临界调控时，生态、供水、防洪防凌、发电量、出力这5个目标中以哪个目标为主，优先对哪个子系统进行调控，各目标间的层次关系如何，这些都是多维临界调控层次需要解决的问题。

分层决策是一种非结构性或半结构性决策，因为系统中有些目标可以用数量特征表示，如供水量、发电量等，而有些目标只能用定性语言来描述，如生态效益、防洪效益等，所以决策过程需要与决策人员进行交流，要借助于人们的某种价值观，采用人机对话方式，通过全面权衡利弊得失，选出“满意权衡方案”。目前，国内外有关多目标决策的方法有灰色关联层次法、集对分析法、层次分析法（AHP）、模糊优选法、SMART法、ELECTRE法等。

对于黄河流域水资源的调控层次，理论上也应该用上述方法来确定，但由于黄河问题比较典型，众多研究者已结合生产实际对相关问题进行了较深入的研究，目前已基本上对各目标的优先等级达成了共识，即先满足防洪防凌要求，然后是生态、供水、上游梯级出力、发电。因此，本文临界调控的层次也按照上述顺序进行，即防洪防凌、生态、供水、出力、发电。

实施多维临界调控主要是根据调控层次的目标分层结构，对调控备选方案，从最顶层目标开始，判断与该目标有关的序参量有序度是否在[0，1]区间，如果不属于该区间则说明序参量不符合临界阈值要求，需要通过实施调控措施进行调控，重新求出相应的临界调控方案。依次对下一层目标进行调控，直到序参量有序度及3个序参量组的有序度在合理范围。如果3个序参量组的有序度在[0，1]区间，但决策者认为该3个序参量组的有序度偏低，或偏高，导致其他3个序参量组的有序度偏低，那么，也需要对3个序参量组的相关序参量进行调控。最后计算水资源系统的有序度熵，如果有序度熵减少，说明调控是可行的，水资源、社会经济、生态环境3个系统趋向于更协调；否则需要进一步采取调控措施进行调控，直至系统熵减小，或者决策者满意为止，调控程序如图8-8所示。

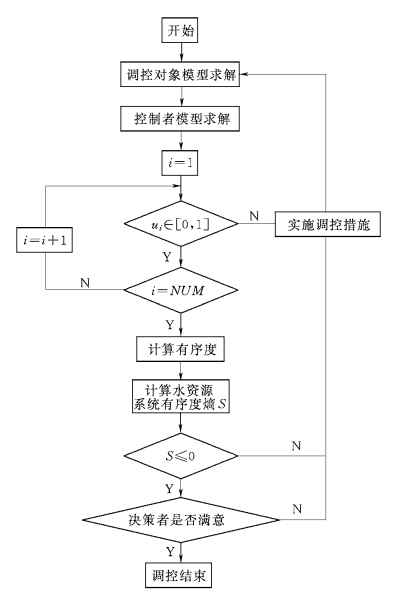
图8-8　水资源多维临界调控程序流程图

图中，i为序参量编号，NUM为序参量个数，ui为序参量有序度，S为水资源系统熵。