3.6.2 BP神经网络的计算过程
BP神经网络的计算过程由正向计算过程和反向计算过程组成。在正向计算过程中,输入信号要先向前传播到隐层节点,经过传递函数后,再把隐层节点的输出信息传播到输出层节点,最后给出输出结果。若网络的输出值与期望值存在误差,则要进行误差反向计算,将误差信号沿原来的连接通路返回,通过修改连接各节点的权值使误差减小。
1.前向计算过程
采用如上的网络结构,当网络中输入层的输出分别是x1,x2,…,xn,根据人工神经元的基本原理,隐层各神经元的输入分别是:
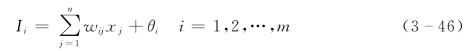
式中:wij为隐层神经元i与输入层神经元j的连接权;θi为隐层神经元的阈值。
选择一定的函数作为隐层神经元的激发函数,则隐层神经元的输出为:
![]()
考虑到Sigmoid函数:
![]()
有如下的特性:
(1)当I信号较小时,也有一定的O值相对应,即输入到神经元的信号比较弱时,神经元也有输出,这样不丢失较小的信息反映。
(2)当I较大时,输出趋于常数,不会出现“溢出”现象。
(3)具有良好的微分特性,即有:
![]()
故选用该函数作为隐层神经元的激发函数。S型函数图像如图3-4所示。
一般,取输出层神经元的阈值为0,另外取比例系数为1的线性函数作为输出层神经元的激发函数,则输出层神经元的输出,也就是整个网络的输出为:
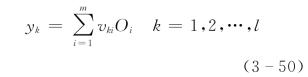
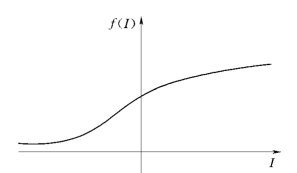
图3-4 Sigmoid函数图像(https://www.daowen.com)
式中:vki为输出层神经元k与隐层神经元i的连接权。
以上公式给出了输出层神经元与隐层神经元的连接权vki组成的向量W,在给出或按照一定的方式确定W值以后,就能够在给出一组网络的输入后,求出网络对应的输出值。
2.反向计算过程
设有学习样本为(x1p,x2p,…,xnp;tkp),n=1,2,…,p;p为学习样本数。对某样本(x1p,x2p,…,xnp;tkp)在给定网络连接权向量W以后,可以计算网络的输出值ykp,定义各输出的误差为:
![]()
并定义样本p的误差函数为:

一般情况下,W的值是随机给出的,因此求得的网络输出值ykp精度不高。在确定网络的结构以后,即在确定网络中隐层神经元数目m的情况下,只能通过调整W的值,逐步降低误差dkp,以提高网络的计算精度。在反向传播过程中,是沿着误差函数ep随W变化的负梯度方向对W进行修正的。设W的修正值为ΔW,取
![]()
式中:η为学习率,取0~1间的数。
将式(3-51)、式(3-52)代入式(3-53)中,得到:
![]()
这里的ΔW为:
![]()
由式(3-55),可以求得样本为p时,ΔW中的元素是:
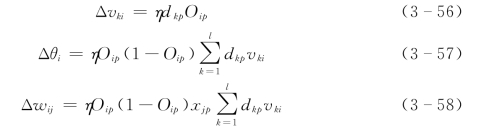
由于在完成正向计算以后,已经求出隐层各神经元的输出Oip和网络的输出误差dp,因此能够使用式(3-56)~式(3-58)求得ΔW的值,最后采用迭代式
![]()
对原W进行修正计算,得到新的连接权向量W。
