3.6.4 BP遗传预测方法
BP算法尽管具有理论上比较成熟,网络结构简单,工作状态稳定,有较强的联想、记忆和推广能力,可以以任意精度逼近任何非线性连续函数等优点,但在需水预测实际应用过程中,发现BP算法存在如下一些问题。
(1)反向传播算法的收敛速度比较慢,一般需要成千上万次迭代计算。
(2)存在能量函数局部极小值。
(3)网络隐层神经元数目的选取和连接权W初值的选取往往靠经验。
(4)新加入的样本要影响到已学习完的样本。
针对以上问题,结合遗传算法提出以下3项措施实现对BP算法的改进。
1.增加附加动量项来改进算法
在式(3-56)~式(3-59)中,确定连接权修正值ΔW的计算过程,实际上是优化计算中的梯度下降法,当能量函数对应的误差曲面为窄长型时,影响了网络的收敛速度,所以可以通过增加附加动量项的方法来改进算法,即取
![]()
式中:ΔW(n)为第n次迭代计算时连接权的修正值;ΔW(n-1)为前一次迭代计算时计算所得的连接权修正值;a为动量因子,一般取接近于1的值。
在式(3-68)中,aΔW(n-1)称为附加动量项,利用附加动量项可以平滑梯度方向的剧烈变化,增加算法的稳定性。在具体计算过程中,学习率η越大,学习速度会越快,但过大时会引起振荡效应;而动量因子a过大可能会导致发散,过小则收敛速度太慢。一般来说,取a=0.2~0.5,η=0.9~0.98,算法的收敛速度较快。
2.改进训练样本的归一化方法
由于BP网络的输入节点物理量各不相同,数值相差甚远,必须对输入的数据进行归一化。数据归一化处理的一般方法是:设样本数据为xp(p=1,2,…,P),定义xmax=max{xp},xmin=min{xp},归一化处理按以下公式计算:
![]()
将样本数据转化为0~1区间的数据,这样可以取较小的数作为网络的连接权ω,网络计算不会发生计算溢出的问题。对网络的输出数据,还可以进行还原计算,恢复实际值。如下:
![]()
但是,考虑到Sigmoid函数在值域[0,0.1]和[0.9,1.0]区域内曲线变化极为平坦,故合适的归一化应是将各输入量归一至[0.1,0.9]区域内,方法为:(https://www.daowen.com)
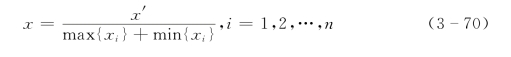
式中:x′、x分别为归一化前、后的样本值;max{xi}、min{xi}分别为x所在单元的样本值的最大值和最小值。
3.引入遗传算法(GA)对BP网络进行优化
遗传算法对神经网络(ANN)优化方式主要有5种,见表3-13。
表3-13 ANN与GA的结合方式
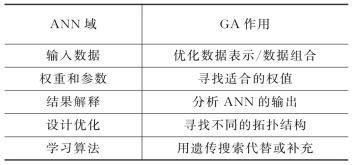
考虑到应用神经网络进行样本的训练时采用的是BP算法,从根本上说在网络结构已固定的情况下,网络训练的目的是为了确定较佳的权值,即权值的确定,从而使式(3-53)所定义的样本总误差达到最小,故采取GA与BP网络进行权重和参数结合方式。遗传BP算法流程如图3-5所示。
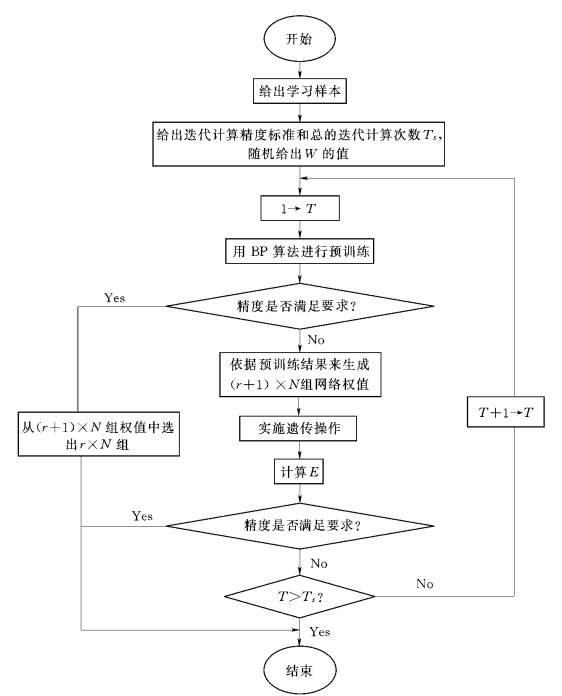
图3-5 遗传BP算法流程图
具体步骤如下。
(1)随机产生N组在不同实数区间内取值的初始网络权值。
(2)用BP算法对这N组初始权值分别进行预训练,若经过训练后这N组权值至少已有一组满足要求,则算法结束;否则转入(3)。
(3)分别依据经过预训练的N组权值所对应的上下限确定取值区间,在区间内随机生成r×N组新的权值,连同经过训练的N组权值一起,构成完整的基因群体,共(r+1)×N组权值。
(4)对这(r+1)×N组权值进行选择、交叉和变异操作。
(5)如果经过步骤(4)的操作已至少得到一组满足精度要求的权值,则算法结束;否则从经过遗传操作的这(r+1)×N组权值中选出N组较好的,回复到(2)。
遗传BP算法流程图中给出总的迭代计算次数Ts是为了避免计算精度一直不满足时程序无法结束问题的发生。
