3.3.4 指数平滑法（确定型）
指数平滑法是利用过去的统计资料以平滑系数来进行预测的。这种方法是对移动平均法的改进和发展，它既考虑对预测期情况有较大影响的最近期的实际统计数据给以较大的权数，给较远期的实际统计数据较小的权数问题，又不像应用移动平均法时需要储存很多的实际统计资料，因此比移动平均法要节省时间。
指数平滑法的特点是以预测对象前期的实际值和前期的预测值为基础，经过修匀处理后得到本期的预测值，所以指数平滑又称指数修匀，可以用来消除预测对象时间序列的偶然性变动。指数平滑法所依赖的原则有两条：一是历史时间越近，数据对未来的影响就越大，反之则较小；二是不断用误差纠正新的预测值，即运用“误差反馈原理”进行修正。其目标就是采用“修匀”历史数据来区别基本数据模式和随机波动，这相当于在历史数据中消除极大值或极小值获得该时间序列的“平滑值”，并以它作为对未来时期的预测值。
1.指数平滑模型
设有需水量序列{yt，t=1，2，3，…，n}，其三次指数平滑模型为：
式中：at，bt，ct均为平滑系数。
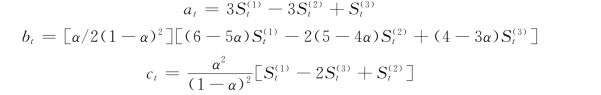
其中：
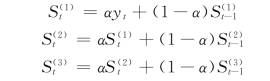
2.指数平滑时加权系数a的确定
运用指数平滑时加权系数a的选择是否得当直接影响着预测效果。
平滑系数α值的传统确定方法为试算法，即以α=0.1为起点，逐次加大，以各种不同的α值去试算。再比较最近几期的追溯预测误差
和估算标准差，选用预测误差和估计标准差较小的α值。在计算机应用比较普及的今天，这种以预测误差最小为标准的试算法还是可行的。但若对时间序列不加分析而直接试算α值，不仅会加大数据输入量与计算工作量，而且也影响预测的有效性与精确性。从预测的简便公式
可知：α值越大，预测值越能反映实际值的变动情况；α取值越小，预测值越接近于前期预测值，即越趋向于某一稳定值。因此在对用水时间序列进行分析的基础上，可依据表3-6确定平滑系数α的取值范围，在取值范围内再采用试算法确定α的具体取值。
表3-6 判断依据
时间序列波动情况可采用曲线图法，在不易判断的情况下，也可先取α值为0.1、0.3、0.6进行试算，选择预测误差最小的α值，在此α值附近确定一区间进行试算。
3.指数平滑法初值S0的确定
在指数平滑法中初值S0的确定也是很重要的，将直接影响预测的结果。初始值S0的确定方法有两种，一种是以第一期实际值X1作为初始值，即
=X1；另一种是以前三期的简单平均数作为初始值，通常采取前三项，即
。传统上认为当参与预测的数据项数大于15时，可以前三项的简单平均数作初始值。
指数平滑模型一般也用于水资源需求的短期预测，相对于移动平均法预测精度要高一些，并且距离起点年越近，预测的相对误差越小，这也充分反映了指数平滑的本质特点：预测模型可充分利用原点的信息，且随着与原点年距离的增加，信息利用量迅速减少，所以短期预测较为可靠。
4.算例
已知黄河流域1971～1999年的需水资料，见表3-7，预测2000年的需水量。
表3-7 黄河流域1971～1999年的需水资料 单位：亿m3
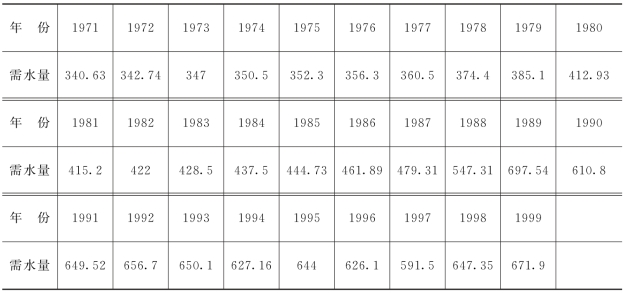
（1）确定初始平滑值S0。
当数据个数大于15个时，可以取初始平滑值
343.46
（2）确定加权系数α。
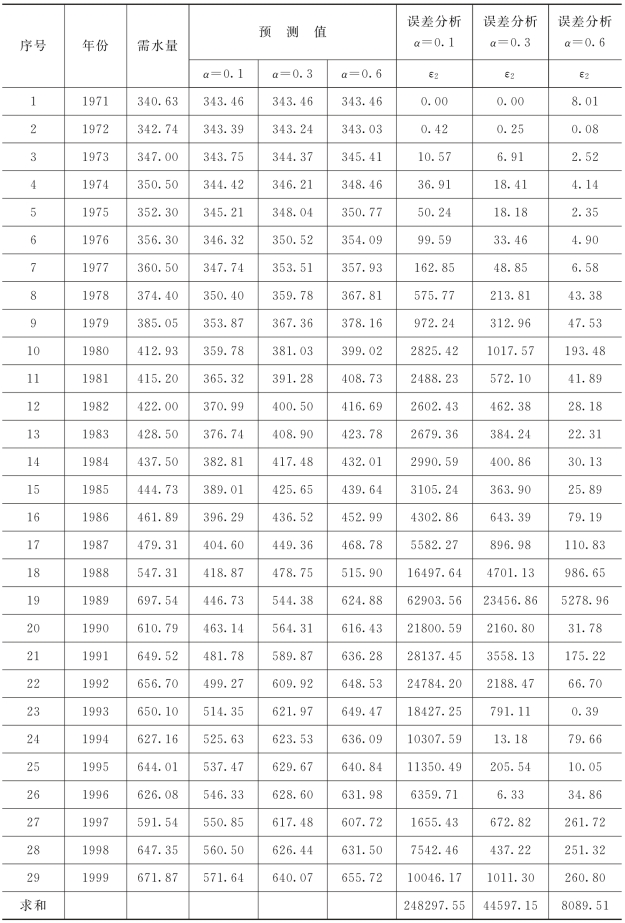
在此我们分别取α=0.1，α=0.3，α=0.6计算平方误差ε2，选取ε2最小的a作为平滑系数。建立误差分析表3-8。
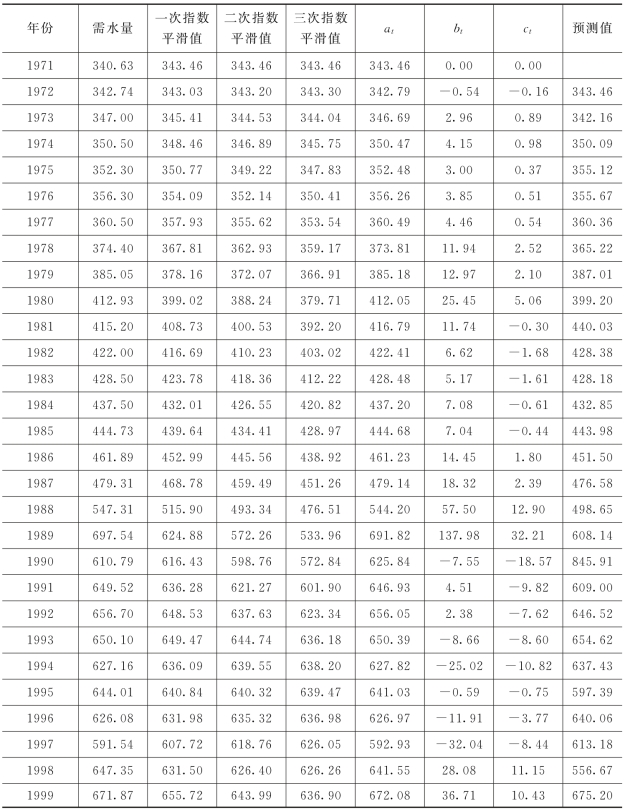
由表3-8分析知，当α=0.6时，平方误差ε2最小。故选取α=0.6。
表3-8 误差分析 单位：亿m3
（3）指数平滑法。
由以上分析得到的α=0.6，S0=X1=340.63，开始做指数平滑计算。计算结果见表3-9。
表3-9 指数平滑法计算结果 单位：亿m3
（4）预测计算。
以1999年为基期，建立指数平滑模型：
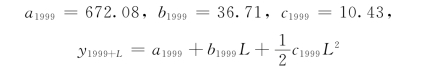
则 