3.4.1 回归分析预测法
3.4.1.1 回归预测法的概念
回归预测法，是分析因变量与自变量之间相互关系，用回归方程表示，根据自变量的数值变化预测因变量数值变化的方法。
在水资源预测中，把水资源需求量当作因变量，把那些与水资源预测有关的因素当作自变量，收集自变量的充分数据，应用相关分析和回归分析求得回归方程，并利用回归方程进行预测。回归预测法中的自变量，与时间序列预测法中的自变量不相同。后者的自变量是时间本身，前者的自变量不是时间本身，而是其他的变量。回归预测法中的自变量与因变量之间，有的属于因果关系，有的属于伴随关系。不能认为只有因果关系才能进行回归预测，实际上伴随关系也是一种相关关系，只要收集大量的足够的资料，也可以用回归预测法进行预测。在回归预测法中，自变量不是随机的或者是给定的，这与相关分析中自变量有所区别。相关分析中的自变量是随机的。
在作回归预测时必须注意下列几个问题，这些问题是提高预测准确度的条件。
（1）必须正确认识社会经济现象之间的内在的必然联系和外部的偶然联系，不为假相关所迷惑。因此，切不可轻视理论分析而草率运用回归预测法。
（2）因变量与自变量之间的关系必须密切，要有强相关，而自变量与另一个自变量之间的关系，必须不密切，要求弱相关或零相关。判断相关关系密切程度的方法，可以通过绘制相关图和计算相关系数。
（3）自变量的预测值必须比因变量的预测值精确或容易求得。因为预测因变量的未来情况，必须有自变量的未来数据代入回归方程式才能计算出来。如果自变量的预测值更难求得，那么该回归方程的应用价值就不大了。
（4）要正确地选择回归方程的形式。亦即选择因变量和自变量的关系式是直线方程式还是曲线方程式，是一个自变量还是几个自变量。另外，还要注意计算简便，易于掌握。
（5）要有简单而又有效的验证方法。
3.4.1.2 回归预测法的种类和步骤
1.回归预测法的种类
（1）一元回归预测。一元回归预测就是用相关分析法分析一个自变量和一个因变量之间的相关关系，利用一元回归方程式进行预测。例如，以居民货币收入预测某种耐用消费品的销售量；以工人劳动生产率预测利润额；以施肥量预测某种农作物的收获率；以人口数量预测某地区的生活用水需求等。
（2）多元回归预测。多元回归预测就是分析一个因变量与若干个自变量的相关关系，建立多元回归方程，以若干自变量的变化预测一个因变量的变化程度和未来的数量状况。例如，以施肥量、气温、降雨量预测某种农作物的收获率；以商业企业的职工劳动生产率和流通费率预测利润率；以降雨、经济、人口等因素预测水资源需求的总量等。
（3）自回归预测。自回归预测就是用一个时间数列的因变量数列与向过去推移若干时期的一个或几个自变量数列进行预测。例如对按月编制的时间数列，用今年1月至12月的数列作为因变量数列，用以前某月至某月的数列作为自变量数列，计算其相关系数，建立回归方程进行预测。
从回归方程的类型看，还可分为线性回归方程预测和曲线回归方程预测两种。
2.回归预测法的步骤
回归预测法的步骤并不是固定不变的，而是非常灵活的。一般有以下几个步骤。
（1）筛选自变量。首先，分析各自变量与因变量之间的相关关系，观察其相关关系的表现形式及密切程度。选用那些与需水量关系最为密切的自变量。在用多元回归预测时，还要分析各自变量之间的相关关系，选用那些关系不密切的自变量。如有两个自变量相互关系很密切，则应舍弃其中的一个。
（2）确定回归方程式。根据理论分析和相关分析，如果有几个重要因素同时对预测对象有影响作用，而且关系密切，可以确定用多元回归方程式；如果其中某一个是基本的，起决定作用的，而其他因素影响作用不大或相关关系不密切，则可以确定用一元回归方程式进行预测。如果自变量和因变量之间的数据分布是线性趋势，可确定用直线回归方程；如果是曲线趋势，可确定用曲线回归方程。回归方程式确定以后，就可求回归方程中未知参数。当参数和自变量的预测值求出后，这个回归方程就可作为以自变量预测因变量的预测公式。
求回归方程式中参数值的方法很多，如可采用最小平方法。
（3）计算相关系数，说明预测结果的可靠程度。相关系数更确切地概括表明自变量对因变量的相关程度。如两者关系密切，则预测结果的可靠性越高；两者关系不密切，则预测结果不很可靠。因此，计算相关系数，可以间接地说明预测结果的可靠程度。
相关系数介于-1与+1之间，计算结果为正数表示正相关，负数表示负相关。
（4）利用回归方程进行预测。通过理论分析和相关系数，如果预测对象（因变量）与影响因素（自变量）之间，确实存在着显著的相关关系，那么过去和现在的用水数据规律，能延续到未来，也就是说，因变量和自变量之间的数量关系，能够反映未来需水的情况。同时，对影响因素（自变量）的情况已作过调查或预测，掌握了自变量在预测期的数据。这样，就可把自变量的数据代入回归预测方程，求得预测对象（因变量）的预测值。
（5）对预测作出置信区间的估计。用回归方程计算出来的预测值，是一个具体的数，称为点预测。点预测值是一个平均数，实际值可能高于或低于它，还必须用一定的几率保证其置信区间的范围。
为了计算置信区间，就要计算预测值的标准误差。其计算公式如下：
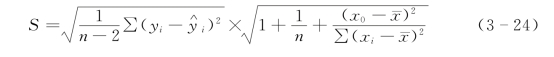
式中：S为标准差；y为因变量的实际值；
为因变量的估计值，即回归方程的计算值；n为数据个数；n-2为自由度，因为只用x、y两个变量，故减2；xi为自变量；
为自变量的平均值；x0为需要计算置信区间的预测点。
式中第一个因素
为考虑自由度后的标准差；第二个因素是调整预测中xi和
的离差程度（即xi和
之差）的。如果确定回归方程的数据个数n很大，而x0接近
，第二个因素就会接近于1，S就等于第一个因素。但是，如果n很小，或预测点xi与
相距较远，式中第二个因素会大于1，预测值的标准误差就比第一个因素大得多。
根据概率论证明，在数据较多时置信区间为：
置信度为68.3%；
置信度为95.45%；
置信度为99.7%。
扩大置信区间，可以增加预测的可靠程度；但如果置信区间很宽，就会使预测结果没有多大意义。