(一)数据与方法
本文用一个面板数据来实证检验省级反腐力度的决定因素。研究的因变量是两个反腐力度的指标:每万名公职人员中被纪委处分的处级以上干部数量,以及每万名公职人员中被检察院立案查办的处级以上干部数量。[34]计算每万名公职人员中的案件数量,是为了确保该数值在不同大小的省份间具有可比性。
反腐数据的主要来源是各省年鉴中纪检机关和检察院的工作报告。其中,纪检机关的年度报告一般会写明某省的各级纪检监察机关所处分的干部人数,以及其中的处级以上干部人数;检察院的年度报告一般会通报被检察院立案查办的处级以上干部人数。据此,我们收集了1998—2008年间31个省级行政单位(以下简称省)的反腐数据。由于并不是每年的工作报告中都包含相关信息,因此实际的观察值数少于11×31=341[35]。由于1997年新修订的《刑法》重新定义了职务犯罪,1997年之后的检察院办案数据和之前不具有可比性[36],因此我们选择1998年作为研究的时间起点。
图3-3显示的是全国范围内反腐执法基本状况的时间变化趋势。
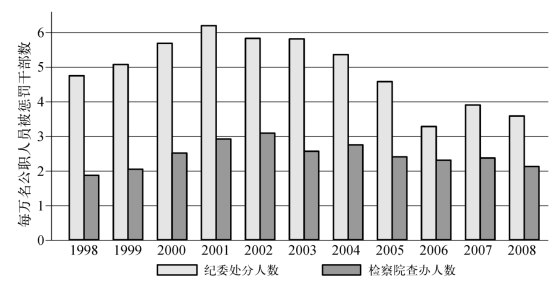
图3-3 历年反腐执法基本状况(31个省级行政单位平均值)(1998—2008年)
可以看出,地方上纪委办案的基本状况在这一时期内有明显的变化。1998年后平均每万名公职人员中被处分的处级干部逐年上升,直到2001年达到峰值,之后在2004—2006年间逐年显著下降,而在2007年又短期回升。相比之下,检察院的办案更为稳定,但也在2001年上升到最高点。当然,取31个省级行政单位的平均值掩盖了每个单位内的力度浮动情况。总得来说,图3-3揭示了反腐执法体现较强的周期性。
我们估计以下的线性回归模型:
yit=α+βxit+γzit+vi+εit
在该模型中,yit代表因变量,vi代表单元的个体特性(unitspecific effects),εit是每个观察值的独特误差项(idiosyncratic error term),xit代表解释变量的矩阵。其中,第一个解释变量为某年某省的省委常委中外来干部的比例。根据假设一,外来干部的比例的增加会导致反腐力度的上升,因此该变量对应的回归系数应为正值。
假设二认为各省的反腐力度应与中央政府对反腐工作的强调程度呈正相关。如上文所述,中央的政策侧重点主要是通过领导人讲话和下发文件的方式传达的。因此,本文选择了三份主要的中央政策性讲话和文件,并在此基础上创建一个综合性的指数来衡量中央对反腐工作的强调。第一份传递中央政策信息的讲话是国务院总理在每年全国人大会议上作的政府工作报告。在工作报告中,反腐只是总理谈论的众多问题中的一项,而在每年的报告中涉及腐败问题的篇幅都不尽相同。有理由认为,当中央将政策重点偏向反腐工作时,工作报告中谈及腐败的比例也会上升。因此,我们阅读了历年的总理工作报告并计算了报告中涉及腐败问题的字数百分比[37]。这是中央政策指数的第一个组成部分。
此外,中共中央纪律检查委员会(中纪委)在每年年初都会召开一次全体会议,布置下一年的工作。在全会上,中纪委书记会依照惯例发表一篇讲话,总结上一年的反腐成绩并强调下一年的工作重点。我们假设,当中央有意提升反腐工作力度时,该讲话的篇幅也会更长。因此,中纪委书记讲话的总字数就被当做中央政策指数的第二组成部分。最后,在全会闭幕前,中纪委都会发表一份全会公报,总结会议内容的同时也宣布会议达成的决议,而这份公报的长度也可以被看成是中央反腐政策的风向标。所以,中纪委全会公报的总字数构成了中央政策指数的第三部分。值得一提的是,所选择的三项政策性文件或讲话都是在年初出台的,所以和当年的实际反腐结果应不存在互为因果的内生性问题。我们先将三项量化指标分别转化为0—1的标准值,再将三个标准值取平均数,即生成中央政策指数。表3-1显示了有关这一指数的相关细节,包括三个组成部分的原始值和0—1标准值。
表3-1 中央对反腐工作的强调指数(1998—2008年)
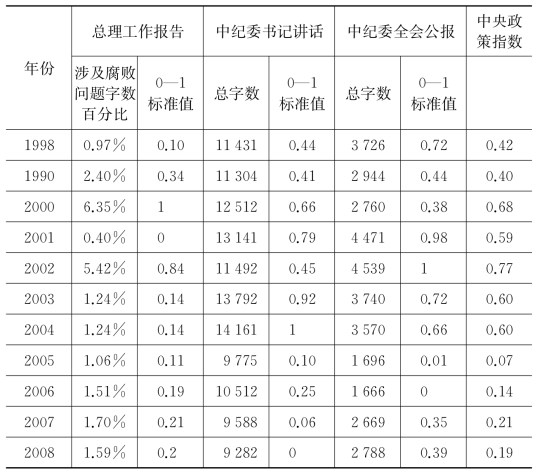
注:总理历年工作报告可在以下网站查到:www.gov.cn/test/2006-02/16/content200719.htm。
中纪委书记讲话和中纪委全会公报收录在《中国监察》刊物中。
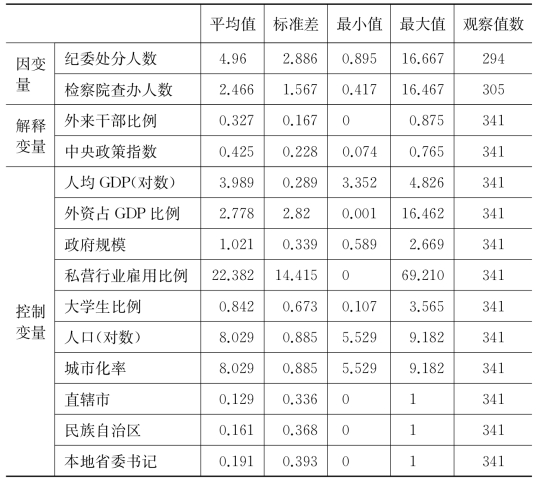
矩阵zit代表的是一系列控制变量。已有文献讨论了各种可能影响腐败程度的社会经济因素[38]。其中,经济的发展带来受教育水平和识字率的上升,使得贪腐行为更容易被揭发和制约。公务员队伍的规模以及政府对经济的干预程度都会影响官员寻租的空间。此外,国内市场向国际竞争的开放程度也可能制约官员的寻租行为。基于这些考虑,本研究包括了以下控制变量:
●该省的人均GDP(取以10为底数的对数)。
●直接利用外资在GDP中的比重。
●政府规模,即公职人员在劳动人口中的比例。
●人口中受雇于私营行业的比例。
●人口中在读大学生的比例。
●人口规模(取以10为底数的对数)。
●城市化率,即劳动人口中受雇于城市的比例。
模型用一个哑变量来代表四个直辖市——北京、天津、上海和重庆。由于直辖市在政治和经济上的特殊重要性,中央可能特别重视对它们的监督[39],由此导致更强的反腐力度。同时,另一个哑变量则代表了五个少数民族自治区。由于在这些地区处理民族关系和反分裂是政策的着重点,地方政府在处理反腐败问题时可能更为谨慎。最后,考虑到省委书记作为一把手,可能在反腐问题上承担主要责任,我们用一个哑变量来代表省委书记的职业背景。当省委书记是一名本地干部时,哑变量取值为1,否则为0。表3-2介绍了各个变量的汇总统计。
表3-2 变量汇总统计
在估计等式(1)中的β时,解释变量中的外来干部比例变量由于存在内生性问题,可能会产生估值的偏差。这是因为,外来干部比例可能影响反腐力度,但如果反腐案件频发,也可能导致中央向该省派驻更多的外来干部。这种“空降”干部的做法既是为了加强该省反腐败力度,也是表达对本地干部的督促。如果外来干部比例和反腐败执法之间存在这样互为因果的关系,最小二乘法(OLS)的估值就会产生偏差。
为外来干部比例找到一个合适的工具变量是相当不易的,因为大多数可能影响外来干部比例的因素,也可能同时影响反腐执行的结果。为解决这一问题,本文选择以1992年各省省委常委中的外来干部比例作为一个工具变量。由于省委班子在五年一次的党代会上往往会做较大调整,1998—2008年间的省委常委人员组成与1992年的班子已经发生了很大变化。同时,省委常委中的外来干部比例在各地都呈现出一定的路径依赖。
如图3-4所示,在1992年有较多外来常委的省份,到了1998—2008年间外来干部比例也较高。因此,我们认为1992年的外来常委比例除了影响后期的外来常委比例之外,不会对1998—2008年间的反腐力度有直接影响。换言之,该工具变量能够满足排斥限制(exclusion restriction)的条件。
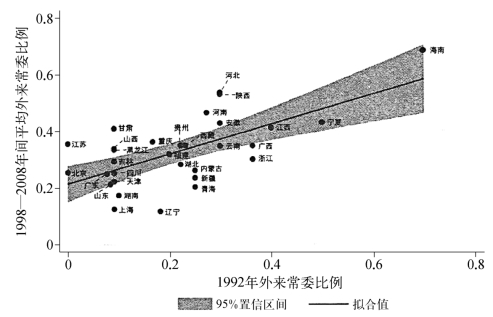
图3-4 1992年外来常委比例与后期外来常委比例的相关性
当以面板数据进行实证分析时,常常面临如何处理每一个单元自身特性(即等式中的vi)所带来影响的问题。比如,每个省份自身的历史、文化或其他无法观测到的特点,可能都会对因变量产生影响。一种解决方法是运用随机效应模型(random effect model),假设单元个体特性是依照某种特定的概率分布。这种方法使模型中可以包含那些不随时间改变的变量。我们将先以随机效应模型进行估计,之后再用固定效应模型(fixed effect model)检验结果的稳健性。此外,考虑到时间序列数据中可能存在的自相关(autocorrelation)现象,分析将使用带有一阶自回归干扰项(first-order autoregressive disturbance)的模型[40]。
