上下级间的方案协商博弈

在上下级间的方案“协商博弈”模型中，我们假定行政区划调整中存在发生互动关系的两级政府。上级政府具有方案的最终决定权，而下级政府具有提出不同方案供协商的商议权。每一级政府在区划调整中都试图实现更大的预期净收益，而两级政府在可能的区划调整方案和预期净收益间的逻辑关系上只具有有限认知能力，这使它们之间存在围绕方案进行协商的可能性。在协商过程中，双方认知能力得以改善，且预期净收益将进行相应调整。我们借助图6-2中的展开式来说明该博弈过程的特点。

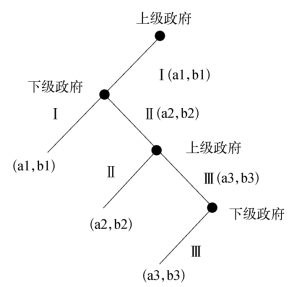
图6-2　两级政府间的方案“协商博弈”

在图6-2中，a表示上级政府的预期净收益，b表示下级政府的预期净收益。（aX，bX）表示上级政府和下级政府的预期净收益组合，其关系为a1＜a2＜a3，b1＜b2，b3≤b2。

在模型中，上级政府首先提出方案Ⅰ，按照方案Ⅰ，两级政府的预期收益是（a1，b1），下级政府将对此方案做出反应。如果是独裁者博弈，那么下级政府只能接受这个方案。但是在我们的模型中，下级政府具有商议权，因此，下级政府具有两个策略：接受方案Ⅰ，或提出方案Ⅱ。如果接受方案Ⅰ，博弈结束；如果提出方案Ⅱ，博弈继续。

对下级政府来说，运用商议权提出的方案Ⅱ，需要既能增加自己的预期净收益，又能对上级政府有利，这样才有现实意义。也就是说，方案Ⅱ的预期收益组合必须具有“a1＜a2，b1＜b2”的特征。如果没有“b1＜b2”，下级政府没有提出新方案的激励；如果没有“a1＜a2”，新方案不足以说服一级政府放弃方案Ⅰ，考虑乃至接受方案Ⅱ。下级政府之所以能够提出对上级政府更有利的方案，主要和上级政府对于区划调整的多种可能方案与预期净收益间的关系只具有有限认知能力相关。

这一轮博弈不同于讨价还价博弈。在我们熟知的讨价还价博弈中，虽然同样存在一方提出方案，另一方相对提出其他方案的情况，但是两个方案所对应的预期净收益在博弈参与者间是此消彼长的，即“a1＞a2，b1＜b2”，而不是协商博弈中的“a1＜a2，b1＜b2”。之所以有此差别，是因为在讨价还价博弈中，博弈参与双方都有退出权，只要合作比退出净收益高，在合作范围内的净收益此消彼长是可以接受的。但在协商博弈中，上级拥有方案的最终决定权，下级方没有退出或拒绝权，只有商议权，因此不可能提出减少拥有最终决定权的上级净收益的方案。

当下级政府提出方案Ⅱ之后，上级政府有两个策略，一是采纳方案Ⅱ，博弈结束；二是从方案Ⅱ受到启发，发现至少对上级政府更好的方案，从而提出方案Ⅲ（由于存在a2＞a1的关系，因此我们假定理性的上级政府不会选择坚持方案Ⅰ）。从净收益的角度看，方案Ⅲ首先具有a3＞a2的特点，这是上级政府提出新方案的激励所在。至于b3的大小，存在各种可能，它可能大于、等于或小于b2。不过在这一模型中，我们设定b3≤b2。之所以如此设定，一是凸显上级政府具有最终决定权，这种决定权使它可以不满足下级政府的净收益要求；二是因为下级政府预期净收益最大化的区划格局，通常对上级政府来说不是最优的（原因详见前述的政府区划决策—收益模型）。

由于对上级政府来说，方案Ⅲ的预期净收益大于方案Ⅱ，因此它的占优策略是提出方案Ⅲ。在模型中，面对方案Ⅲ，下级政府选择接受，博弈就此结束。就现实性而言，下级政府如果有使上级政府和自身预期净收益都增加的方案，序贯博弈还可能继续下去。但这里的逻辑和前述下级政府提出方案Ⅱ时相同，故出于模型简化的考虑，此处不再赘述。