政府区划决策-收益模型
在行政区划调整过程中，直接相关的主体就是上级政府和其辖区内的下级政府，因而我们把区划调整分析中的行动主体分为两类，即上级政府和下级政府。在本节，上级政府和下级政府都限于地方政府范围。我们假定，不论上级政府还是下级政府都追求其预期净收益（即总收益和总成本的差额）的最大化。此处的政府收益，既包括政府获得的可支配资源，也包括其治理活动获得的社会赞许，是政府自身对这二者综合价值的评估。显然，政府收益并不等同于其辖区的全社会收益。另外为简化起见，我们将上级政府和下级政府都视为整体行动者，而不区分政府内各部门、各类官员的行为策略与收益差异。
从中国当前的等级区划体制着眼，区划调整主要涉及两个方面：（1）区划空间范围的调整；（2）辖区级别位序的调整。空间范围与辖区级别位序这两个因素，都影响着政府的净收益。据此，在其他条件给定的前提下，政府与区划相关的净收益函数可以表示为：
式（1）中，NRi表示某级地方政府的净收益，si是该地方政府的辖区空间范围，li为辖区级序（级别位序）。自变量li是一个定序变量，对任何一级地方政府来说，辖区级序越高，潜在可支配资源越多，因而净收益是辖区级别的增函数。自变量si是一个连续变量，它和地方政府净收益间的关系比较复杂，需要展开论述。
在我们的模型中，假定上级政府的辖区范围不变，但下级政府的区划范围可能改变，其变化不仅影响下级政府的净收益，也影响着上级政府的净收益。下级政府的净收益直接受自身区划范围的影响，上级政府的净收益则受下属各政府辖区分布状态的影响。
为简化起见，我们假定随自身辖区面积的扩大，下级政府的边际净收益具有先递增后递减的倒U型变动特点。这一特点和下级政府辖区治理的边际成本随面积增加先递减、后递增有关。同时假定在上级政府辖区范围内，设立多个下级政府比只设立一个下级政府获得的边际净收益要更大。可以用图6-1来表示这种关系。
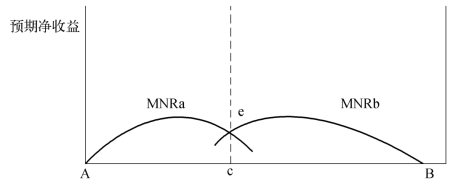
图6-1 区划与两级地方政府的净收益
在图6-1中，假定某地区的上级政府管辖2个下级政府，即下级政府A和B。为方便说明，我们将二维的面积用一维的线段表示，横轴从A到B的线段表示整个地区的面积。由A点越向右意味着下级政府A的区划面积越大；由B点越向左意味着下级政府B的区划面积越大。纵轴表示预期净收益。MNRa是A的预期边际净收益曲线，MNRb是B的预期边际净收益曲线，e点为两条曲线的交点。在e点处，MNRa=MNRb，下级政府A和B的总和预期净收益达到最大。假定上级政府的预期净收益与下级政府A、B的总和预期净收益正相关，那么上级政府的预期净收益在e点最大。通过e点做垂线相交于横轴的c点，就是上级政府划分下级政府区划的最优点。对上级政府来说，不论将规划线确定在ec线的左侧还是右侧，其预期净收益都将受到损失。
由上面的阐述可知，上级政府调整下级政府区划，使自身预期净收益最大化的条件是各下级政府辖区面积的预期边际净收益相等。用公式表达如下：
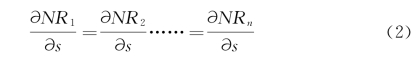
式（2）中，
为下级政府辖区面积的边际净收益。公式（2）也可以记成：
如果上级政府的预期净收益不是和下级政府的总和预期净收益正相关，那么情况就要复杂一些。这时，上级政府调整下级行政区划使自身预期净收益最大化的条件是：各下级政府辖区面积为上级政府提供的预期边际净收益相等。但从形式角度看，只要将
或MNR视为下级政府辖区面积为上级政府提供的预期边际净收益即可。其道理相同，故不再赘述。
需要注意，虽然MNRa=MNRb是上级政府的最优规划条件，但对下级政府而言，只要其预期边际净收益仍大于零（即MNR＞0），就没有实现自身预期净收益的最大化。事实上，现实中的区划调整，在假定满足公式（2）的同时，使所有下级政府均实现“MNR=0”是不存在的。因此在图6-1中，我们设定e点对应的MNRa和MNRb均为正。这意味着，即使假定上下级政府对净收益大小的评价是一致的，e点也不是稳定的均衡点，下级政府有偏离这一点的激励。
上面的论述虽然只涉及一个上级政府，但也可以扩展到两个乃至多个上级政府区划决策的情况。当下级政府区划的调整不仅要经过其直接的上级政府决定，而且要经过更上级的政府决定时，追求自身净收益最大化的更上级政府也会基于上述原则考虑下级政府的区划调整对其收益造成的影响。