4.2.2 复利分析
由于复利更全面、更准确地反映资金的时间价值，因此，在经济分析中全部按复利法计算和分析投资方案的各项经济指标。复利分析就是对存款与贷款这种投资活动进行分析，直接分析这种简单投资活动中资金的时间价值，并在此基础上建立工程经济分析的基本思路。
4.2.2.1 复利分析的基本公式
由资金等值的概念可知，复利计算即为等值计算。普通复利公式是指以年复利计息，按年进行支付的复利计算公式，根据支付方式和等值换算时点的不同，可分为若干类，分述如下。
1.一次支付复利公式
设本金为P（一次支付），利率为r，F为本利和，n为计算利息的期数，通常以年计。
那么：
第1期末的本利和F1=P（1+r）
第2期末的本利和F2=F1（1+r）=P（1+r）2
…
第n期末的本利和Fn=Fn-1（1+r）=P（1+r）n
于是，我们就得到一次支付复利公式为：
式中，习惯上把F称为本金P在n期末、年利率为r的终值，本金P称为初值或现值，系数（1+r）n称为一次支付复利系数，简称复利系数，用符号（F/P，r，n）表示。由此可知，终值F是由现值乘以复利系数得到的。反之，现值P可由终值F乘以系数（1+r）-n得到，即：
式中，系数（1+r）-n称为折现系数（或贴现系数），用符号（P/F，r，n）表示，为了简化计算工作，人们编制出对于不同r和n值的复利系数和折现系数表，以备查用。
2.等额支付复利公式
等额支付的意思是每个时间周期所支付的金额是相等的。常把每期发生相同的本金称为年金。若每期末发生的年金是A，每期的利率为r，期数为n，按复利计息，则n期年金A的本利和总额称为期末发生的复利年金终值。那么：
第1期末年金A的终值F1=A（1+r）n-1
第2期末年金A的终值F2=A（1+r）n-2
…
第n期末年金A的终值Fn=A
对以上每一期末年金A的终值求和，于是就得到所要求的复利年金终值为：
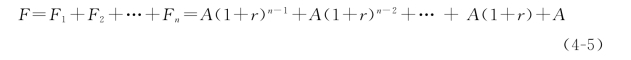
即
式中，系数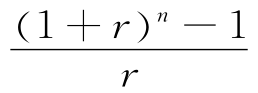
称为年金复利系数，用符号（F/A，i，n）表示。
对上式乘以折现系数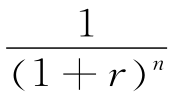
，则将复利年金终值F折算为期末发生的复利年金现值P，即
或
式中，系数
或
都称为等额支付系列折现系数（或贴现系数），也称为年金现值系数，用符号（P/A，r，n）表示。
3.变额支付复利公式
把每期发生的不相同的本金称为变额年金，仍以A表示，那么根据变额年金的变化方式，可分别计算其终值和现值。
（1）等差变化。
设每期变额年金的变化规律是按等差（d）数列的规则变化。记n期末年金终值为F，则有：
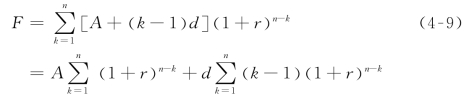
（2）等比变化。
设每期变额年金按等比（q）数列的规则变化。n期末年金终值F为：
4.2.2.2 名义利率和实际利率
以上的复利利息计算中，把1年作为利息周期，这种按年计的利率就称为名义利率。但在实际工作中有时会出现按半年、季度，甚至1个月计息，因此，1年可分为若干个计息期，名义利率除以1年的计息次数所得的商就称为计息期实际利率（或有效利率）。如年利率6%，每半年复利计息1次，即名义利率为6%，实际利率为6%÷2=3%，其计息期为6个月，1年的计息次数为2。
若1年的计息次数为m，复利计息，那么就称1年所获的利息与本金之比为实际年利率，用字母i表示。m=1时，实际年利率就是名义利率。
1.离散式复利
按期（年、季、月）计息的方式称为离散式复利。1年中计息期数越多，则实际年利率就比名义利率大。设名义利率为，1年中计息k次，则1年末的本利和为：
那么实际年利率为：
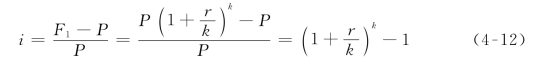
上式反映了以离散式复利计算的实际利率与名义利率的关系，在经济分析评价中被广泛应用。
2.连续式复利
按计息周期为无穷小计息的方式称为连续式复利。此时，一年中的计息数趋于无穷大，则年末的本利和为：
那么实际利率为：
其中e=2.71828。
若现值P为时间t的函数，用P=P（t）表示，以连续复利计算，则终值F亦为t的函数，即：
反之，若F=F（t），则以连续贴现计算的现值为：
如果一个工程项目的现金流量是时间t的函数C（t），而且折现是连续发生的，那么这个工程项目自开始至n年末的现值可用以下积分式表示：
由于资金具有时间价值，所以项目实施带来的费用和效益，不仅与其货币的多少有关，而且与其发生的时间有关。利用前面介绍的复利公式，可将一笔资金按一定的利率在不同时刻做等值变换，也可以将一笔资金等值变换到任何时刻，或等值变换为任何一种支付形式。这正是复利分析的意义所在。