5.3.1　解析法

5.3.1　解析法

1.随机变量独立时的风险分析

设净现金流量Cj=（j=0，1，2，…，n）是相互独立的随机变量，并令PW满足如下关系：

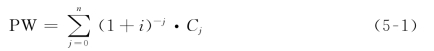
式中，PW为净现值；i为利率；n为计息期或项目周期。

则有：

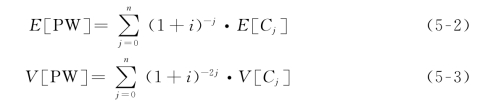
式中，E［Cj］为随机变量的期望值；E［PW］为净现值的期望值；V［PW］为随机变量的方差；V［Cj］为净现值的方差。

2.随机变量与时间相关时的风险分析

设净现金流量是一组非独立（与时间有关）的随机变量。在这种情况下，为简化起见，可把每年的净现金流量分解成2个分量，一个是逐年独立的现金流量xj，另一个是与时间相关的现金流量yj，则第j年的净现金流量Cj为：

式中，xj对yj是独立的。Yjk对j是相关的，对k是独立的，即y0k，y1k，…，ynk是相关的，而yj1，yj2，…，yjm是独立的。则净现值的期望值和方差可按下式计算：

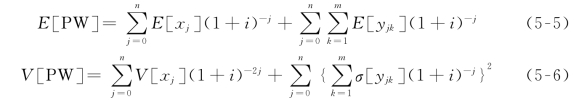
式中，E［xj］，E［yjk］分别为随机变量xj，yjk的期望值；V［xj］为随机变量xj的方差；σ［yjk］为随机变量yjk的标准差。