1.3.1 旋转矩阵的用法
2026年01月15日
1.3.1 旋转矩阵的用法
旋转矩阵R(见图1.11)有三种用法(见图1.12)。
1)描述一个坐标系相对于另一个坐标系的姿态。
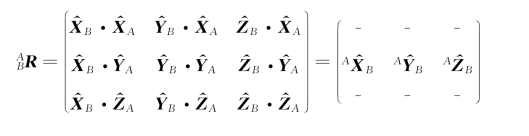
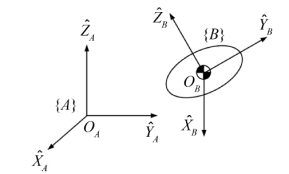
图1.11 旋转矩阵
2)对于一个点P,由其在坐标系{B}中的表达转换到坐标系{A}中的表达。其中坐标系{A}与坐标系{B}仅有相对转动。
A P=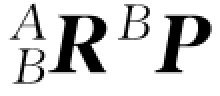 (见图1.12)
(见图1.12)
推导证明:
在初始坐标系{B}中,点P 的坐标:
![]()
在新坐标系{A}中,点P 的坐标:

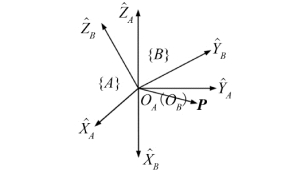 (https://www.daowen.com)
(https://www.daowen.com)
图1.12 {B}坐标系转换到{A}坐标
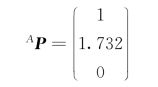
结果如图1.13所示。
3)点P 在绕着坐标系的某一坐标轴旋转,得到新的点P′(见图1.14)。
A P′=R(θ)A P
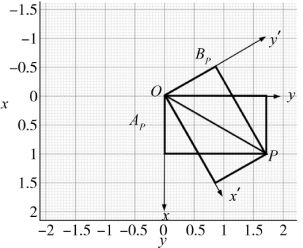
图1.13 上视图验证
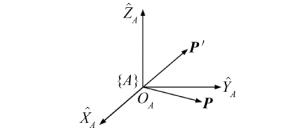
图1.14 点P在同一坐标中转动

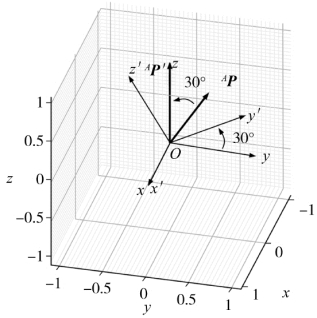
图1.15 A P 求解

