6.2.4 神经网络控制
1)神经网络理论介绍。
径向基函数神经网络(radial basis function neural networks,RBFNNs)起源于20世纪80年代。1985年,Powell提出了多变量插值的径向基函数,并证明该函数可以应用于任意维度的离散和连续数据集中进行插值和拟合运算。径向基函数又称为RBF函数或高斯函数,是一种适于大规模样本的非线性拟合函数。1988年,Moody和Darken提出了以RBF径向基函数为激活函数的新型神经网络,称为RBF神经网络(见图6.8),它能够以任意精度逼近任意连续或离散函数,特别适合于解决各类非线性问题的预测和分类问题。RBF神经网络属于单隐层前馈神经网络,其输入层与其他神经网络相同,输入层到隐含层再到输出层经历了三次运算。
(1)从输入层到隐含层求解输入节点与类别标签的欧式距离![]()
(2)在隐含层根据欧式距离使用RBF高斯函数进行曲线拟合。
(3)从隐含层到输出层为一个线性函数。如果是预测,则使用最小二乘法的正规方程组。
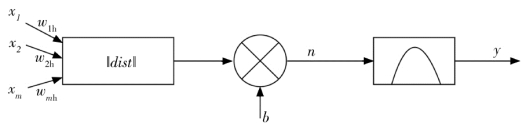
图6.8 径向基神经元模型
径向基网络中常用的激励函数为高斯函数:

Cover定理:将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。这就是RBF(径向基函数)神经网络的原理。用RBF作为隐单元的“基”构成隐含层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分问题在高维空间内线性可分。详细一点就是用RBF的隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间。通过RBF的中心点来确定这种映射关系。而隐含层空间到输出空间的映射是线性的,即网络输出是单元输出的线性加权和,此处的权即为网络可调参数。
RBF神经网络结构与BP(反向传播)神经网络结构类似,也是一种三层网络。第一层是输入层,仅仅起到传输信号的作用,输入层和隐含层之间可以看作连接权值为1的连接。第二层为隐含层,隐含层节点数视所描述问题的需要而定,如果用于预测,那么隐含层单元数与样本数应相同。隐含层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负线性函数,该函数是局部响应函数。RBF的非线性函数包含两部分:首先对输入样本计算欧式距离;接下来对距离进行RBF拟合。第三层为输出层,它一般是一个线性函数,对隐含层的输出数据进行线性权值调整,采用的是线性优化策略。与BP神经网络相比,RBF神经网络减少了误差反馈的权值更新环节,仅在隐含层使用高斯函数作为激活函数拟合数据集的非线性,而网络输出调整是线性的,因而学习速度比BP神经网络要快很多,并能够避免局部极小问题。
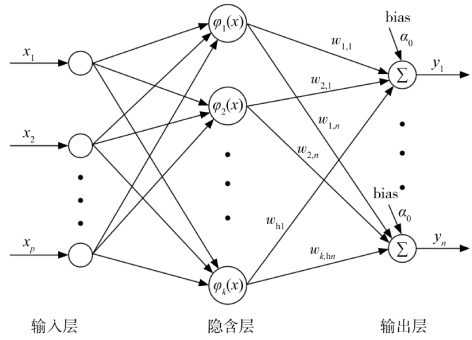
图6.9 多输入多输出的RBF神经网络结构
从径向基函数神经网络的结构中可得到网络输出为:
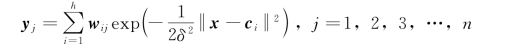
其中,x=(x 1,x 2,…,x p)T为网络输入,c i为网络隐含层结点的中心,w ij 为隐含层到输出层的连接权值,i=1,2,…,h 为隐含层的结点数,y j 为与输入样本对应的网络的第j个输出结点的实际输出。
因为RBF神经网络的作用函数为高斯函数,其作用域只在有限的数值区间内,所以RBF神经网络是局部逼近的。但是RBF神经网络的学习速度非常快,且不会出现局部极小问题,非常适用于飞行器控制等对实时性要求高的控制系统,并可以有效地提高控制系统的自适应性和鲁棒性。
下面将采用自适应RBF神经网络控制实现飞行器的位置、姿态跟踪控制。其中自适应RBF神经网络可以在整个飞行过程中在线地、有效地估计各通道中未知的模型参数和持续的外界干扰;跟踪误差是最终一致有界的,同时上界值的大小可以控制;基于Lyapunov的自适应律可以保证RBF神经网络在线训练以及补偿飞行过程中变化的参数,确保飞行系统的稳定性。
2)基于RBF神经网络的控制器的设计。
(1)位置控制器的设计。考虑飞行器的平移运动模型以及参数不确定性和外界干扰等,平移运动动力学模型给出如下:

根据上述飞行器的位置轨迹跟踪问题,设计自适应RBF神经网络,完成飞行器的自主轨迹跟踪控制。首先定义系统的跟踪误差为:
![]()
其中,ζr(t)是给定的位置轨迹,然后定义辅助的状态误差向量γζ(t),便于后续控制器的表述和稳定性的分析。
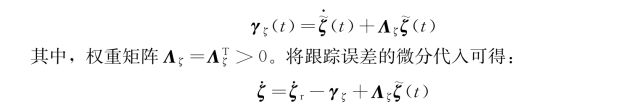
考虑模型、跟踪微分误差以及辅助误差信号,可求得出辅助误差信号的微分为:

设计自适应RBF 神经网络, 估计和补偿未知的多输入多输出函数, 即使用RBFNNs来估计未知的连续函数fζ,并保证跟踪误差最终收敛到足够小的区域集里,该神经网络结构如图6.10所示。
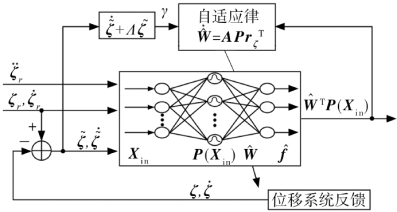
图6.10 自适应RBF神经网络位置控制结构
其中,RBF神经网络的输入是期望位置轨迹ζt 及其一阶、二阶微分,和飞行器的位置状态量ζ 及其速度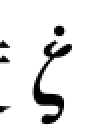 ;神经网络的多变量输出是:
;神经网络的多变量输出是:
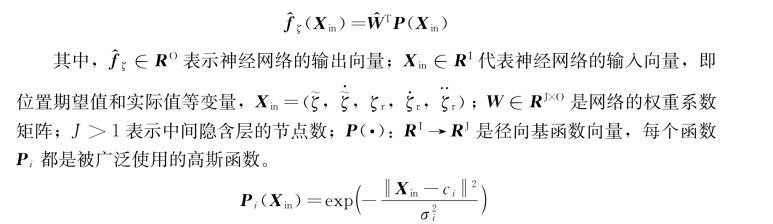 (https://www.daowen.com)
(https://www.daowen.com)
其中,c i 是第i个神经元的中心位置;σi 是第i个神经元的宽度,表示该神经元的作用域。存在最优权重值,使得神经网络的逼近结果满足:
![]()
假设εmax >0表示神经网络的逼近误差ε 的最大值。考虑四旋翼飞行器的平移运动学模型,以及RBF神经网络的结构,设计控制律:
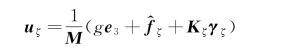
为了提高飞行控制的实时性,引入了自适应算法进行权值的在线调整,控制表达式如下:
![]()
其中,Kζ 是正常数矩阵;A 是正定的对称矩阵,表示自适应增益。根据此控制律,即使存在不确定的系统参数或者外界扰动,飞行器的位置跟踪和速度跟踪也可被保证。
下面将位置控制中的水平控制器输出转换为期望姿态角,考虑到旋翼飞行器的实际飞行安全,对滚转角和俯仰角的范围给出如下约束条件:
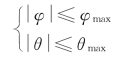
作如下变量代换:

(2)姿态控制器的设计。考虑飞行器的旋转运动模型以及参数不确定性和外界干扰等,旋转运动动力学模型给出如下:

根据上述飞行器的姿态角跟踪问题,设计自适应RBF神经网络,完成飞行器的自主姿态跟踪控制。首先定义姿态系统的跟踪误差为:
![]()
其中ηr(t)是期望姿态角,然后定义辅助的状态误差向量γη(t),便于后续控制器的表述。

考虑模型、跟踪微分误差以及辅助误差信号,可求得出误差信号的微分为:
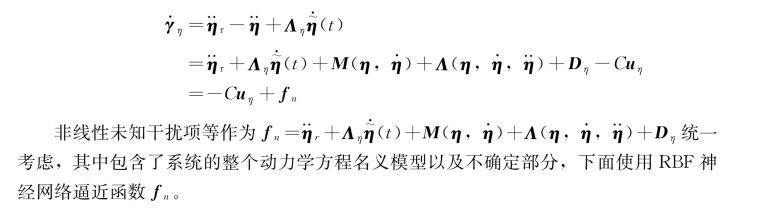
设计自适应RBF 神经网络, 估计和补偿未知的多输入多输出函数, 即使用RBFNNs来估计未知的连续函数f n,并保证跟踪误差最终收敛到足够小的区域集里,该神经网络结构如图6.11所示。
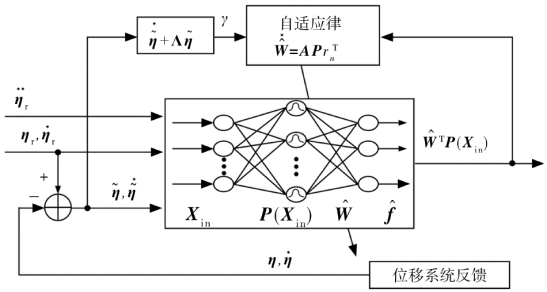
图6.11 自适应RBF神经网络姿态控制结构

其中,c i 是第i个神经元的中心位置;σi 是第i个神经元的宽度,表示该神经元的作用域。存在最优权重值,使得神经网络的逼近结果满足:
![]()
假设εmax >0表示神经网络的逼近误差ε 的最大值。考虑四旋翼飞行器的平移运动学模型,以及RBF神经网络的结构,设计控制律:
![]()
为了提高飞行控制的实时性,引入了自适应算法进行权值的在线调整,控制表达式如下:
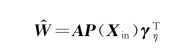
其中,Kη 是正常数矩阵;A 是正定的对称矩阵,表示自适应增益。根据此控制律,即使存在不确定的系统参数或者外界扰动,飞行器的姿态角跟踪和角速度跟踪可被保证。
综上所述,结合基于自适应RBF神经网络的位置控制和姿态控制,可根据期望控制信号(x r,y r,z r,ψr)得到4个控制律(u 1,u 2,u 3,u 4),进而根据旋翼飞行器的飞行特性将其转换为各旋翼的转速信号。
