7.2.4 机载操作臂逆运动学
为求出要求的关节角以放置相对于工作台坐标系｛S｝的工具坐标系｛T｝，可将这个问题分为两部分：首先，进行坐标变换求出相对于基坐标系｛B｝的腕部坐标系｛W｝；然后运用逆运动学求关节角。
求解操作臂运动学方程是一个非线性问题。 已知0N T 的数值， 试图求出θ1，θ2，…，θn。同任何非线性方程组一样，我们必须考虑其解的存在性、多重解问题以及求解方法。
1）解的存在性。
解是否存在完全取决于操作臂的工作空间。简单地说，工作空间是操作臂末端执行器所能到达的范围。若解存在，则被指定的目标点必须在工作空间内。有时对工作空间的定义也很有用：灵巧工作空间指机器人的末端执行器能够从各个方向到达的空间区域。也就是说，机器人末端执行器可以从任意方向到达灵巧工作空间的每一个点。可达工作空间是机器人至少从一个方向上有一个方位可以到达的空间。显然，灵巧工作空间是可达工作空间的子集。
现讨论图7.6所示两连杆操作臂的工作空间。如果l 1＝l 2，则可达工作空间是半径为2l 1 的圆，而灵巧工作空间仅是单独的一点，即原点。如果l 1≠l 2，则不存在灵巧工作空间，而可达工作空间为一外径为l 1＋l 2、内径为
的圆环。在可达工作空间内部，末端执行器有两种可能的方位，在工作空间的边界上只有一种可能的方位。
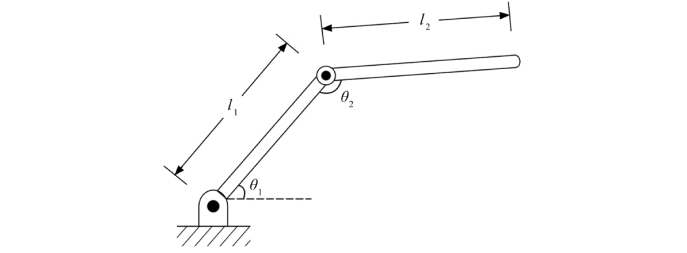
图7.6 连杆长度为l 1 和l 2 的两连杆操作臂
这里讨论的两连杆操作臂的工作空间是假设所有关节能够旋转360°，这在实际机构中是很少见的。当关节旋转角度不能达到360°时，显然工作空间的范围或可能的姿态数目相应减小。例如，对于图7.6所示的操作臂，θ1 的运动范围为360°，但只有当0≤θ2 ≤180°时，可达工作空间才具有相同的范围，而此时仅有一个方位可以达到工作空间的每一个点。
当一个操作臂少于6个自由度时，它在三维空间内不能达到全部位姿。显然，图7.6中的平面操作臂不能伸出平面，因此凡是Z 坐标不为0的目标点均不可达。在很多实际情况中，具有4个或5个自由度的操作臂能够超出平面操作，但显然不能达到全部目标点。必须研究这种操作以便弄清楚它的工作空间。通常这种机器人的工作空间是一个子空间，这个空间是由特定的机器人工作空间确定的。一个值得研究的问题是，对于少于6个自由度的操作臂来说，给定一个确定的一般目标坐标系，什么是最近的可达目标坐标系。
工作空间也取决于工具坐标系的变换，因为所讨论的工具端点一般就是我们所说的可达空间点。一般来说，工具坐标系的变换与操作臂的运动学和逆向运动学无关，所以一般常去研究腕部坐标系｛W｝的工作空间。对于一个给定的末端执行器，定义工具坐标系｛T｝，给定目标坐标系｛G｝，去计算相应的坐标系｛W｝。接着我们会问：｛W｝的期望位姿是否在这个工作空间内？ 这里，我们所研究的工作空间（从计算的角度出发）与用户关心的工作空间是有区别的，用户关心的是末端执行器的工作空间（｛T｝坐标系）。
如果腕部坐标系的期望位姿在这个工作空间内，那么至少存在一个解。
2）多重解问题。
在求解运动学方程时可能遇到的另一个问题就是多重解问题。一个具有3个旋转关节的平面操作臂，由于从任何方位均可到达工作空间的任何位置，因此在平面中有较大的灵巧工作空间（给定适当的连杆长度和大的关节运动范围）。图7.7所示为在某一位姿下带有末端执行器的三连杆操作臂。虚线表示的是可能的位形，在这个位形下，末端操作器的可达位姿与实线所示的位形相同。
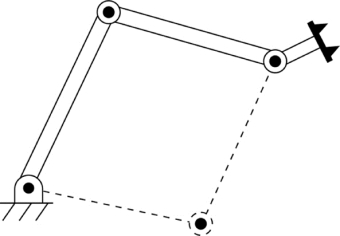
图7.7 三连杆操作臂
因为系统最终只能选择一个解，因此操作臂的多重解现象会产生一些问题。解的选择标准是变化的，然而比较合理的选择应当是取“最短行程”解。例如，在图7.8中，如果操作臂处于点A，我们希望它移动到点B，最近解就是使得每一个运动关节的移动量最小。因此，在没有障碍的情况下，可选择图7.8中上部虚线所示的位形，这表明对于机械臂的当前位置来说只需要对逆运动学程序输入一个小位移量即可。这样，利用算法能够选择关节空间内的最短行程解。但是，“最短行程”解可能有几种确定方式。例如，典型的机器人有3个大连杆，附带3个小连杆，姿态连杆靠近末端执行器。这样，在计算“最短行程”解时需要加权，使得这种选择侧重于移动小连杆而不是移动大连杆。在存在障碍的情况下，“最短行程”解可能发生干涉，这时只能选择“较长行程”解——为此，一般我们需要计算全部可能的解。这样，在图7.8中，障碍的存在意味着需要按照下方虚线所示的位形才能到达B 点。
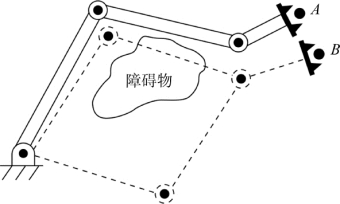
图7.8 运动关节移动量
解的个数取决于操作臂的关节数量，它也是连杆参数（对于旋转关节操作臂来说有αi、αi和d i）和关节运动范围的函数。例如，PUMA560机器人到达一个确定的目标有8个不同的解，图7.9所示为其中的4个解，它们对于手部来说具有相同的位姿。对于图中所示的每一个解，存在另外一种解，其中最后三个关节变为另外一种位形，如式（7-1）所示：
总之，对于一个操作目标共有8个解。由于关节运动范围的限制，这8个解中的某些解是不能实现的。
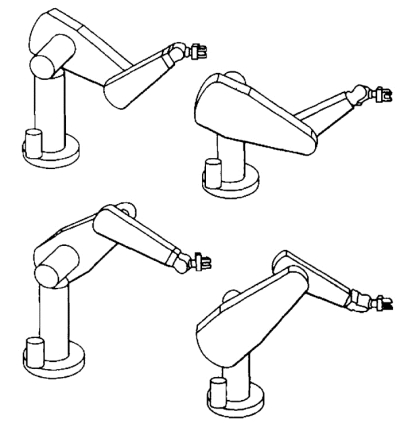
图7.9 PUMA560的4个解
通常，连杆的非零参数越多，达到某一目标的方式也越多。以一个具有6个旋转关节的操作臂为例，图7.9表明解的最大数目与不等于零的连杆长度参数（αi）的数目有关。非零参数越多，解的数目就越多。对于一个全部为旋转关节的6自由度操作臂来说，可能多达16种解。