2.6.3 旋翼无人机的动力学模型
四旋翼飞行器控制器设计的基础是飞行器的动力学模型,前文我们已经阐述过可以把四旋翼飞行器看作刚体来进行研究,且飞行器的重心与机体坐标系的原点重合,忽略飞行器运动时由螺旋桨和电机产生的振动,以及飞行器受地面效应的影响。
在上述假设下,四旋翼飞行器的运动可分为:重心沿惯性坐标系X,Y,Z 三个坐标轴的线运动,以及绕惯性坐标系三个坐标轴的转动,即滚转、俯仰、偏航。对于四旋翼飞行器,大多数研究人员都是依据角动量守恒定律和牛顿第二定律进行飞行器的动力学建模。
根据牛顿第二定律可知,建立四旋翼飞行器的动力学方程如式(2-39)所示:
![]()
其中,m 为整个飞行器的总质量,包括供电设备(铿电池)和机架、螺旋桨电机等的质量,因此飞行器的质量不会发生改变;F 为飞行器运动过程中所受的合外力。
飞行器所受的外力包括重力、阻力、升力。
其中ˉG=(0,0,g)T∈R 3为重力向量(g=9.8 m/s2,为重力加速度)。在机体坐标系中,单个螺旋桨所产生的升力为:

式(2-41)是在惯性坐标下建立的物理方程式,因此要把两个物理方程式统一在同一坐标系中,利用线速度转换矩阵R(Θ)∈R 3×3,统一到惯性坐标系中,如式(2-42):
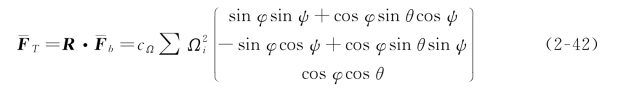
飞行器在运动的过程中受到的阻力为:

化简整理得:
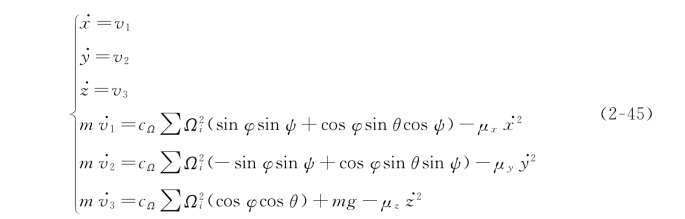
式(2-45)为四旋翼飞行器的线性位移的运动数学模型。根据角动量守恒定律,惯性坐标系下飞行器的转动方程式如式(2-46)所示。

飞行器的角速度向量和飞行器的姿态向量有如下关系:
![]()
则式(2-47)化简整理可得:
![]()
其中,M B 为机体坐标系下的合外力矩。
四旋翼飞行器在运动过程中,螺旋桨的旋转除了给飞行器提供一个向上的升力外,每个螺旋桨还产生一个扭矩。设旋翼到重心的距离大小为l,且四个旋翼与重心的距离都相等,则每个旋翼所产生的力矩大小为:(https://www.daowen.com)
![]()
由四旋翼飞行器的飞行原理可知,俯仰力矩大小为:
![]()
滚转力矩大小为:
![]()
偏航力矩大小为:
![]()
其中,λ 为比例系数,其大小由旋翼半径、空气密度、叶片数等决定。
在四旋翼飞行器运动过程中,当飞行器的飞行姿态发生变化时,对于高速旋转的螺旋桨和直流无刷电机的转子,由于陀螺效应会产生一个附加的无法避免的陀螺力矩,其数学表达为:
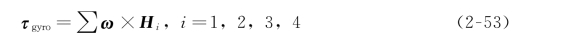
其中H i 为总动量矩,定义J r 为绕z 轴转动的惯量,动量矩的数学表达式为:
![]()
将式(2-54)代入式(2-53)化简整理得:
![]()
则四旋翼飞行器的总合外力矩为:
![]()
将式(2-49)(2-50)(2-51)(2-56)代入式(2-48)化简整理得:
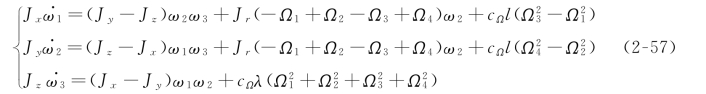
由式(2-47)得到机体角速度与姿态的方程如下:
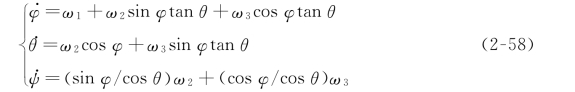
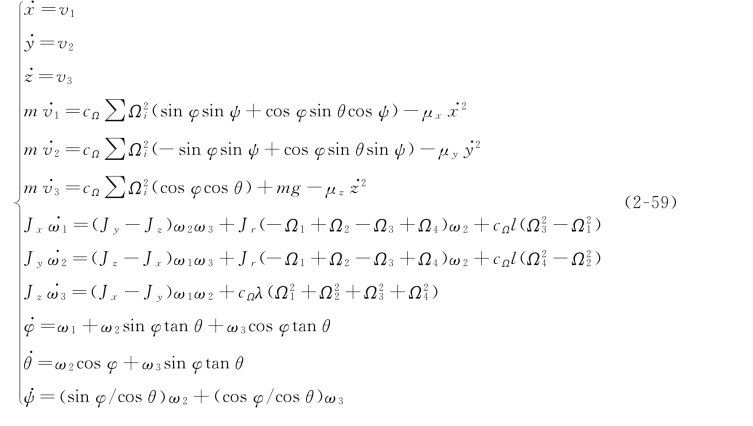
综上所述,四旋翼飞行器的运动学方程为:
