7.6.4 基于笛卡尔空间的控制系统
1)与基于关节空间控制方法的比较。
在此之前所讨论过的所有操作臂的控制方法中,都假定期望轨迹可以用关节位置、速度和加速度的时间历程来表达。已知这些期望输入是有效的,我们设计了基于关节空间的控制方法,这种方法是通过计算关节空间的期望值与实际值之差,从而得到轨迹误差。为了便于研究,我们经常希望操作臂的末端执行器沿直线或其他在笛卡尔坐标系中描述的路径运动。如第7.5节所述,可以计算与笛卡尔坐标下的直线路径相对应的关节空间轨迹的时间历程。图7.26为这种操作臂轨迹控制方法的示意图。这种方法主要是一个轨迹变换过程,用于计算关节轨迹,然后通过某种基于关节坐标的伺服控制实现轨迹跟踪。

图7.26 具有笛卡尔路径输入的基于关节空间的控制方法
如果用解析方法完成轨迹变换过程,那是相当困难的(按照计算费用来说)。需要计算:
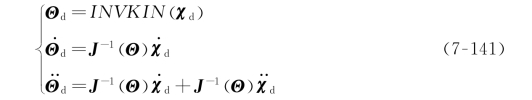
在当前的系统中完成这种计算,通常应用逆运动学方法求解Θd,然后用一阶和二阶差分的数值计算方法求出关节速度和加速度。但是,数值微分容易将噪声放大并引起延迟,除非采用一个专门的滤波器。因此,我们希望找到使计算式(7-141)计算量较小的方法,或者给出一种不需要这些信息的控制方法。
另一种方案如图7.27所示。在这里,检测到的操作臂位置立即由运动学方程变换成笛卡尔坐标下的位置,将它与期望的笛卡尔坐标位置进行比较,得到笛卡尔空间下的误差。这种基于笛卡尔空间误差的控制方法称为基于笛卡尔空间的控制方法。为简明起见,在图7.27中未标识速度反馈,但它在任何情况下都是存在的。
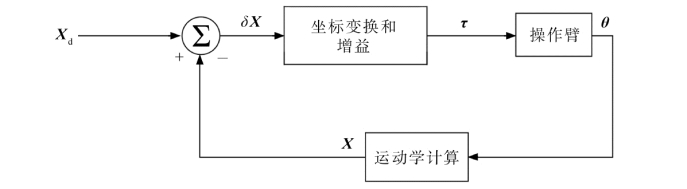
图7.27 基于笛卡尔空间的控制方法示意图
轨迹变换过程可被伺服环中的坐标所代替。注意,基于笛卡尔坐标控制器的许多计算必须在反馈环内部进行,即运动学计算和其他变换现在都是在反馈环内部进行的。这是基于笛卡尔坐标方法的一个缺点。这种系统与基于关节空间系统相比,运行时的采样频率较低。通常情况下这会降低系统的稳定性和抗干扰性能。
2)笛卡尔空间的直接控制方法。
我们很容易得出一种直观的控制方法,见图7.28。这种方法是将笛卡尔空间位置与期望位置比较,得到笛卡尔空间下的误差δX。当控制系统正常工作时,这个误差可以被认为很小,并可以用雅可比方法映射成关节空间内的小位移。将得到的关节空间误差δX 乘以增益来计算使误差减小的转矩。注意,为简明起见,图7.28所示的简化控制器中省略了速度反馈部分,速度反馈可以直接附加到图中。这种方法构成的控制器称为逆雅可比控制器。
另一种容易想到的方法如图7.29所示。这种方法是将笛卡尔空间误差矢量乘以增益来计算笛卡尔坐标系下的力矢量。可以将这个力矢量看成施加在机器人末端执行器上的一个笛卡尔空间的力,它使末端执行器向着笛卡尔空间误差减小的方向运动。将这个笛卡尔坐标系下的力矢量(实际上是一个力-力矩矢量)通过雅可比转置矩阵映射成当量关节力矩,这样可以减小观测到的误差。这种方法构成的控制器称为转置雅可比控制器。
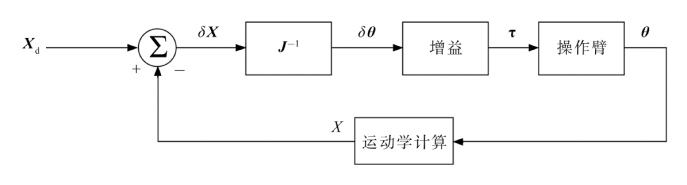
图7.28 逆雅可比笛卡尔空间控制方法(https://www.daowen.com)
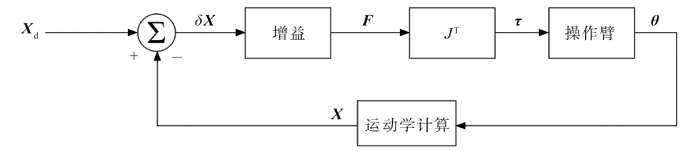
图7.29 转置雅可比笛卡尔空间控制方法
逆雅可比控制器和转置雅可比控制器都是直观的控制方法,难以确定这些方法是否稳定。这些系统的精确的动力学特性是很复杂的。事实是,这两种控制方法都能够工作,但工作性能不太好,都可以通过选择适当的增益使系统工作稳定,包括某种形式的速度反馈。然而它们都不是精确的控制方法,即我们无法选择固定的增益来得到固定的闭环极点。这两种控制器的动力学响应都会随着操作臂位形的变化而变化。
3)笛卡尔空间解耦控制方法。
与基于关节空间控制器一样,基于笛卡尔空间的控制器也应该使操作臂在所有位形下的动力学误差均为常量。而在基于笛卡尔空间控制方法中,误差是在笛卡尔空间表示的,这表明对于所设计的系统,应使其在所有可能的位形下,都可将笛卡尔空间误差限制在临界阻尼状态。
正如基于关节空间的控制器一样,一个性能优良的笛卡尔空间控制器的前提条件是操作臂的线性化和解耦模型。因此,我们必须用笛卡尔坐标的变量写出操作臂的动力学方程。这可以用第7.4节中讨论的方法实现,得到的运动方程形式与关节空间的方程十分相似。刚体动力学方程可以写作:
![]()
其中,F 为作用在机器人末端执行器上的虚拟操作力-力矩矢量,χ 是一个适当表示末端执行器位置和姿态的笛卡尔坐标矢量,M x (Θ)是笛卡尔空间的质量矩阵,![]() 是笛卡尔空间的速度项矢量,G x (Θ )是笛卡尔空间的重力项矢量。
是笛卡尔空间的速度项矢量,G x (Θ )是笛卡尔空间的重力项矢量。
与前面处理基于关节坐标的控制问题一样,可以在一个解耦和线性化控制器中应用动力学方程。因为已知从式(7-142)计算出作用在机器人末端执行器上的虚拟笛卡尔力矢量F,那么就可以使用雅可比转置矩阵来实现这个控制——也就是说,用式(7-142)计算出F 后,实际上已无法将一个笛卡尔空间的力施加到末端执行器上,相反,应用式(7-143)就可计算出能够有效平衡系统的关节力矩:
![]()
图7.30所示为完全动力学解耦的笛卡尔空间操作臂控制系统。注意转置雅可比是在操作臂之前。可看出,图7.30所示的控制器可以直接描述笛卡尔路径而不需要进行轨迹变换。
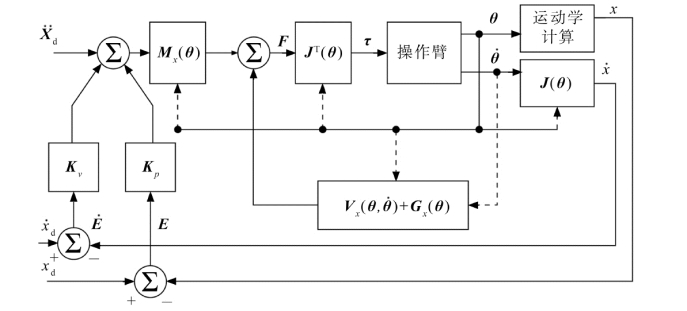
图7.30 基于模型的笛卡尔空间控制方法
与关节空间的情况相同,在实际应用中最好使用双速率控制系统。图7.31所示为一个基于笛卡尔坐标系的解耦和线性化控制器示意图,其中的动力学参数只是操作臂位置的函数。这些动力学参数由后台或另一台控制计算机在一个低于伺服速率的频率下更新。这个方案是比较合理的,因为我们希望伺服频率尽量快(可能为500 Hz或更高),以便最大限度地抑制干扰和保持稳定性。由于动力学参数只是操作臂位置的函数,因此只需在一个能够跟得上操作臂位形变化的速率下更新它们的值。参数更新频率可能不需要高于100 Hz。
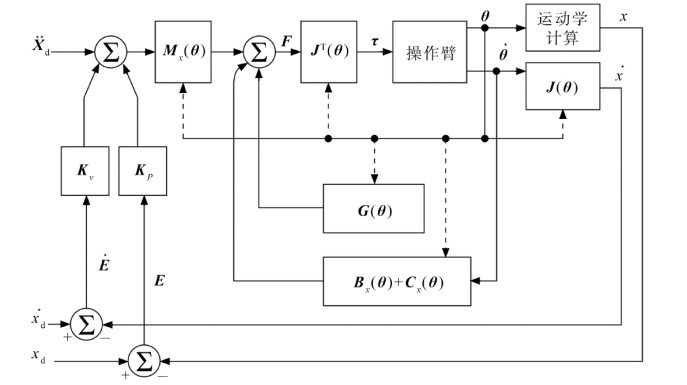
图7.31 基于模型的笛卡尔空间控制的实现方法
