6.2.2 反步法控制
1)反步法原理。
Back stepping法又称反步法、反演法、回推法,它是一种鲁棒递推设计方法,它是从离控制输入量最远的那个方程开始,通过一步一步地对子系统进行设计,向着控制输入“步退”(step back)的方法。即从位于最后的一级开始设计,使其达到渐进稳定,以后再对包括最后一级在内的前一级进行设计,使达渐进稳定,依次类推,直到完成整个控制系统的设计。而各级的稳定性证明是基于Lyapunov函数的方法,整个控制系统则通过逐级累加得以证明。
反步法设计过程清晰,集系统化、结构化于一体,易于实现,对于高阶非线性系统有优越性,它可以保留系统中的有用的非线性。而且容易与鲁棒或自适应控制结合应用于不确定系统(内部特性变化或外部扰动)。但也存在潜在的问题,如对系统结构有严格要求,推导出的控制量的控制参数多且数学表达式复杂等。
为了说明反步法的基本原理,考虑参数严格反馈的单输入单输出(非线性系统)。
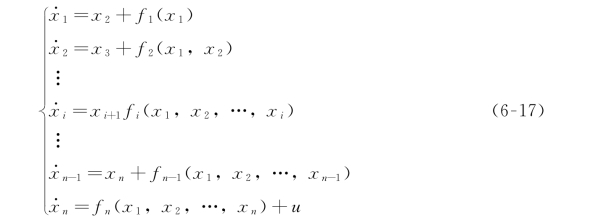
系统结构示意图可以表示如图6.6所示。
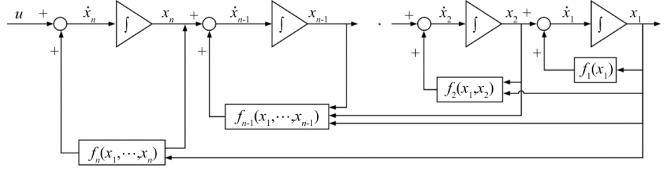
图6.6 系统结构示意图
下面我们对以上系统进行反步控制器设计。
步骤1:

步骤2:
定义Lyapunov函数:
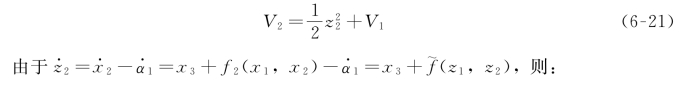

步骤i:
定义Lyapunov函数:
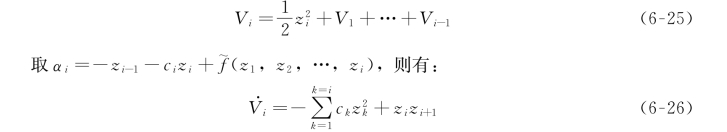
步骤n:
应用上面的定义,我们有:
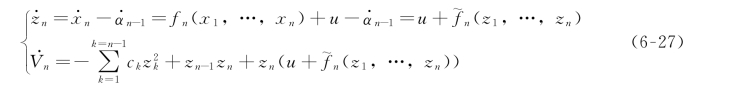
选取控制律为:
![]()
则:

其中,c k(k=1,2,…,n)为正常数。
通过n 步推导最后得出控制律表达式,使得系统的每个子系统满足了Lyapunov稳定理论条件,从而保证系统具有全局意义下的渐进稳定性。
2)基于反步法的控制器的设计。
考虑到机身的内部耦合复杂性、系统模型的非线性和外界干扰的不确定性因素,本次设计采用由位置控制和姿态控制构成的双闭环控制系统,结合反步法和Lyapunov函数来设计鲁棒控制律,即以Lyapunov稳定性理论为基本思想,设计每个子系统所对应的虚拟控制律用于正定,然后通过一步步地迭代,最终获得系统的实际控制信号。其中位置控制器将被划分为3个二阶子系统——x 通道、y 通道和z 通道,每个子系统均采用基于反步法的鲁棒控制,x 通道和y 通道的控制信号u x,u y 可转换为姿态指令信号——期望滚转角(φd)、俯仰角(θd),z 通道的控制信号u 1 即为u 1;同样地,姿态控制器也是分3个二阶子系统来设计控制律,从而得到姿态控制信号(u 2,u 3,u 4)。最后,根据飞行器性能特点,油门控制信号u 1 和姿态控制信号(u 2,u 3,u 4)通过姿态解耦就能得到4个电机的转速控制信号,从而控制飞行器按照指令运行。

(1)位置控制器。将位置子系统看作3个二阶的子系统,分别用于控制飞行器三轴方向上的平移运动,每个二阶的子系统都是严格反馈控制,根据期望信号和对应反馈信号结合反步法和Lyapunov函数来设计鲁棒控制律。在该位置控制器中,输入信号为控制指令信号中的期望位置(x 7d,x 9d,x 11d),所需的反馈信号为飞行器实时三轴位置(x 7,x 9,x 11)和三轴线速度(x 8,x 10,x 12),同时也需要用到当前时刻飞行器的姿态信息(x 1,x 2,x 3),它们都可由IMU以及GPS等传感器的测量值通过姿态解算和组合导航计算得到。位置控制器输出信号为油门控制信号u 1、期望滚转角φd 和期望俯仰角θd。
以高度控制器为例:
z 通道的状态空间方程为:
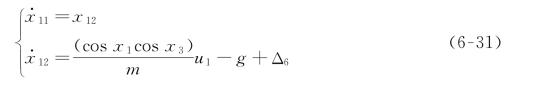
引入误差状态向量:

则:

其中,α11 为x 11 的虚拟控制量;x 11d 为x 11 的期望控制量,即期望高度z r。(https://www.daowen.com)
第一步,设计虚拟控制量α11。
考虑z 11 的Lyapunov函数及其导函数:

第二步,设计U 1 系统的鲁棒控制律。
考虑子系统(z 11,z 12)的Lyapunov函数及其时间的导数:
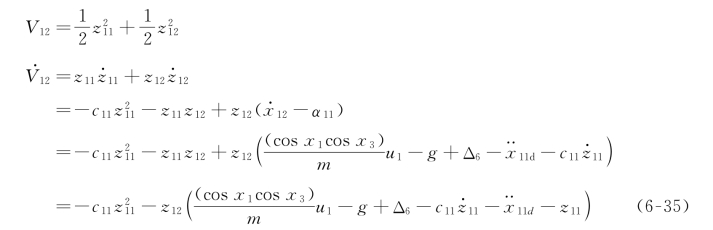
此时,设计U 1 系统的鲁棒控制律为:
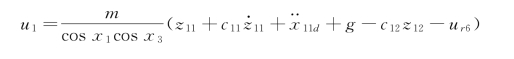

水平坐标x,y 通道的状态空间方程为:
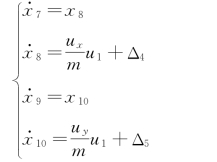
同理,可以得到u x 的鲁棒控制律为:

位置控制器的输出为高度控制信号即u 1 和滚转通道、俯仰通道的指令信号(φd,θd)。所以,需要将x 通道和y 通道控制信号u x,u y 进行如下转换。
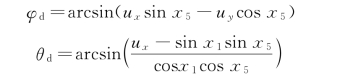
系统运行过程中考虑到四旋翼飞行器的安全飞行,对滚转角和俯仰角的范围给出如下约束条件:
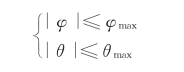
作如下变量代换:

(2)姿态控制器。将姿态子系统看作三个二阶的子系统,分别用于控制飞行器绕三轴的旋转运动。显然,每个二阶的子系统都是严格反馈控制。
以滚转角控制器为例:
φ 通道的状态空间方程为:
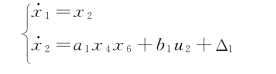
引入误差状态向量:

其中α1 为x 1 的虚拟控制量;x 1d 为x 1 的期望控制量,即在位置控制器中得到的期望滚转角φd。
第一步,设计虚拟控制量α1。
考虑z 1 的Lyapunov函数及其导数:


第二步,设计U 2 系统的鲁棒控制律。
考虑子系统(z 1,z 2)的Lyapunov函数及其导数:

θ,φ 通道的状态空间方程为:
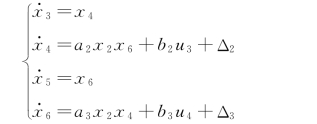
同理,可以得到U 3 系统的鲁棒控制律为:

同样的,U 4 系统的鲁棒控制律为:

