5.4 A* 算法
A* 算法是一种经典的启发式全局搜索算法，是建立在Dijkstra和BFS算法基础上最短路径搜索算法。
Dijkstra算法也称单源最短路径算法，它主要依据从一个节点出发到达有向图中的其余各节点的最短路径，通过整合获得最终的全局路径。Dijkstra算法为每个节点v 记录每一阶段从起始节点S 到v的最短路径，算法的执行主要维护了两个节点集S 和Q 的存取操作。其中集合S中记录了当前已知的具有最小d[v]值的节点（d[v]表示从S到v的最短路径，若路径不存在，则d[v]＝∞），而集合Q 中则存储了其余的节点。初始状态下，集合S＝null，而后每一步都将从Q 中选出d[u]值最小的节点u 并将其移动到S，此时外接边（u，v）获得了拓展。
BFS算法也称作广度/宽度优先搜索算法，BFS算法试图搜索整张图，不对结果的可能位置做任何估算或者假设。在图G＝（V，E）中每一条边e搜索并获得根节点s所能到达的顶点v，并且计算s到v的距离，寻求最短距离（最少边数），当树访问完成所有的顶点（集合）V 时，则终止算法。
A* 算法综合以上Dijkstra算法和BFS算法两者的优点，其代价函数的表达式为：
其中，f（n）（evaluation function）表示从起始节点经当前节点到目标节点的代价；g（n）表示从起始节点到任意节点n的实际距离（实际代价），它表示的是Dijkstra算法原理；h（n）表示从任意节点n 到目标节点的估算距离（估算代价），作为一个启发值，它表示的是BFS算法原理。由于h（n）是一个关于距离的估算值，因此对应地可将任意节点n 到目标节点的实际距离表示为h*（n），其值满足式（5-3）的基本要求，即任意节点n 到目标节点的估计距离值h（n）不得超出其实际距离值h*（n）。
本书中f（n），g（n），h（n），h*（n）等函数均采用欧几里得距离（Euclidean distance）来表示。
当任意点n 的坐标为（x n，y n，z n），它的下一个位置点n＋1的坐标为（x n＋1，y n＋1，z n＋1）时，航迹规划的目标函数为：
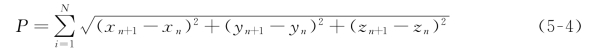
其中，P表示航迹结果，N 为点的个数，（x i，y i，z i）为点的坐标。通过求目标函数极值将在规划中确定出来一系列离散的点，依次连接，并通过平滑处理后即可获得最终的航迹结果。