5.7.2 A* 与人工势场融合算法
A* 算法是一种经典的启发式全局搜索算法，是目前最快的计算最短路径的算法。其优点是适用范围广，不存在局部极值问题，具有启发函数使搜索效率高。但所产生的路径由一系列直线段构成，平滑性和可跟踪性较差。
人工势场法是一种基于虚拟力场的局部路径规划算法。其优点是结构简单，实时性好，在动态避障和平滑控制方面应用广泛。但容易陷入局部最优解产生死锁现象。
本文综合考虑这两种算法的优缺点，将A* 算法路径最短但平滑性差的特点和人工势场法平滑性好但易陷入局部最优的特点结合起来，先建立栅格地图使用改进A* 算法规划出一条初步路径，然后进行关键点优化，将改进A* 算法的关键点设为人工势场的中间目标点，再使用人工势场法平滑相邻两点的路径，最后得到一条路径较短、平滑性较好的安全路径。在MATLAB中进行路径仿真并与单独使用A* 算法和单独使用人工势场法的路径进行比较。
1）A* 势场法的实现。
先根据三维地图利用栅格法进行环境建模，使用改进的A* 算法进行初步路径规划，利用改进的估价函数选择集中最小的点作为当前节点，更新OPEN 集中的相邻节点并将当前节点设为它们的父节点，直到CLOSED集中出现目标节点搜索结束，遍历父节点得到初步规划路径，再进行关键点优化得到由一系列关键点构成的折线路径，在此基础上使用人工势场法进行路径平滑。
针对旋翼式无人飞行器在三维环境下的A* 势场法算法流程图如图5.22所示。
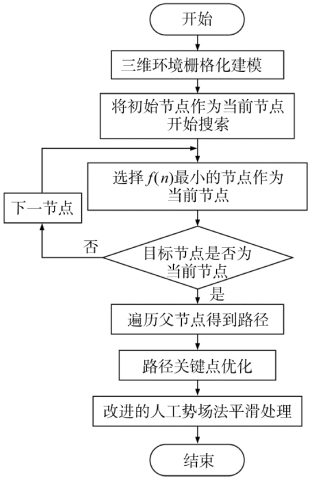
图5.22 A* 势场算法流程图
2）基于A* 势场法的路径仿真。
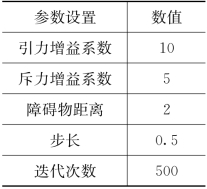
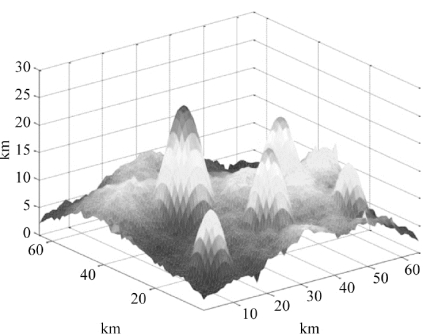
为了证明本文所提出融合算法的可行性与优越性，在三维环境下利用MATLAB进行飞行路径仿真。三维环境地图如图5.23所示，地图由五个山峰和随机地表组成，山峰坐标分别为（10，10），（40，25），（35，50），（20，35），（15，50），飞行设置起点位置为（1，45，11），终点位置为（64，12，12）。A* 势场法仿真参数具体设置见表5-5。
首先，比较使用曼哈顿距离的传统A* 算法与融合算法，由图5.25～图5.27可知，传统A* 算法所产生的路径由若干直线段连接构成，平滑性和可跟踪性差，在使用人工势场法进行路径平滑处理后，路径长度减小，平滑性和可跟踪性显著提高。再比较使用欧几里得距离的改进A* 算法与融合算法，由图5.28、图5.29可得出相同结论。
其次，比较传统A* 算法与改进A* 算法，由图5.24、图5.25、图5.27（a）、图5.28（a）和图5.29（a）可知，启发函数使用欧几里得距离比曼哈顿距离所产生的路径长度更短，转折更少，相对平滑性更好。再比较传统A* 势场法与改进A* 势场法，由图5.26、图5.27（b）、图5.28（b）和图5.29（b）可得出相同的结论。
表5-5 势场法仿真参数设置
图5.23 三维环境地图
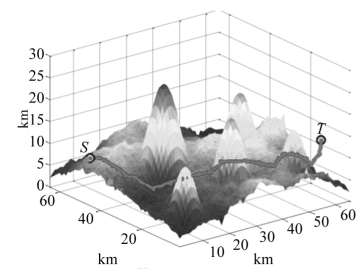
图5.24 人工势场法路径仿真图
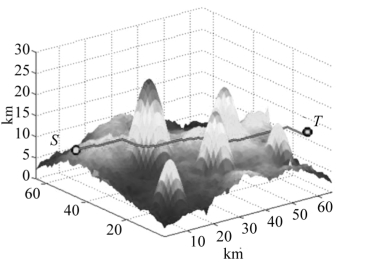
5.25 传统A* 算法路径规划仿真图
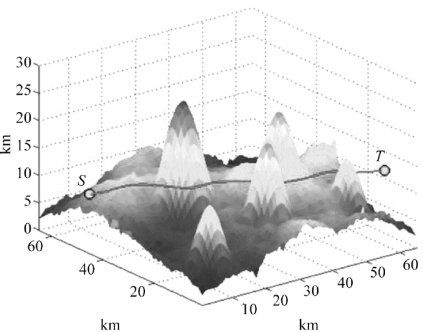
图5.26 融合算法仿真结果（全局图）
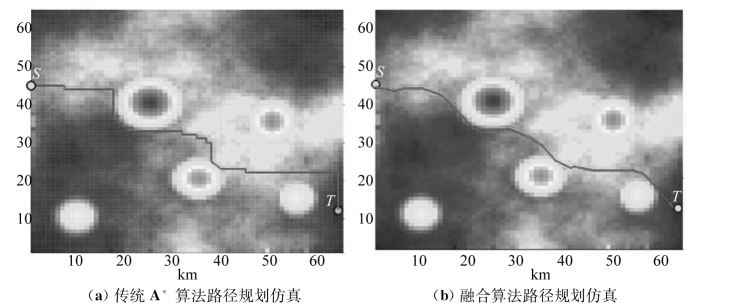
图5.27 传统A* 算法与融合算法仿真结果（俯视图）
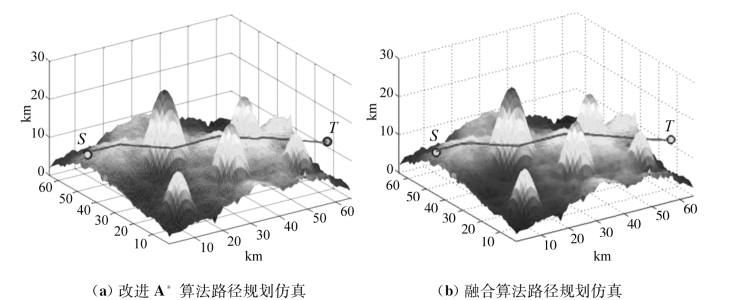
图5.28 改进A* 算法与融合算法仿真结果（全局图）
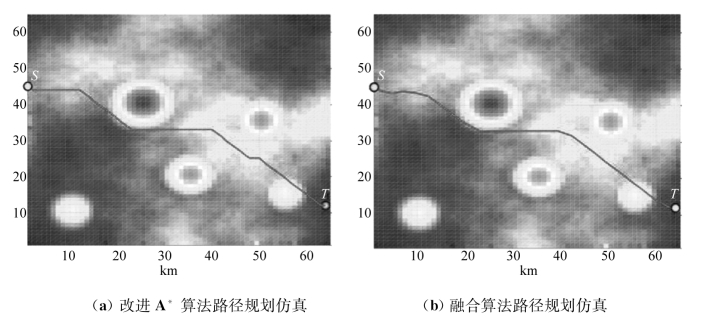
图5.29 改进A* 算法与融合算法仿真结果（俯视图）
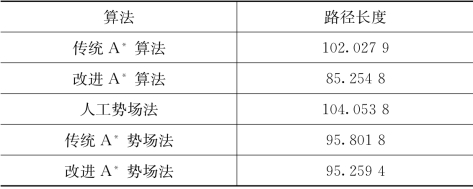
由此可以证明：本节提出的对A* 算法和人工势场法的改进，以及两者的融合算法具有可行性与优越性，融合算法可以在三维山地环境中寻找到一条路径较短且平滑性较好的安全路径，结果见表5-6。
表5-6 路径长度
