4.2 相机标定
相机的精确标定是无人机位姿精确求解的必要条件。对于单目视觉来说，相机标定就是获取相机内参以及畸变参数；对于双目视觉来说，既要获取内参也要获取外参。当然，相机标定在OPENCV或MATLAB中都有现成的函数，只要知道如何调用就可以了。但是之所以单独列出一节，是为了让读者可以透过函数看到外表下的内涵。
在了解标定过程之前，我们需要了解到图像坐标系是如何与世界坐标系联系在一起的，并且坐标系之间的关系不仅仅关乎标定过程，还是视觉定位的原理及其基础。这个过程需要一步一步地分析，我们试图通过摄像机坐标系来搭建一个桥梁。在此之前，为了方便读者理解，先列出一些名词的解释。
世界坐标系（x w，y w，z w）：是目标物体位置的参考系。除了无穷远，世界坐标可以根据运算方便与否自由放置。
相机坐标系（x c，y c，z c）：是摄像机站在自己角度上衡量的物体的坐标系。摄像机坐标系的原点在摄像机的光心上，z 轴与摄像机光轴平行。
图像坐标系（x，y）/（u，v）：是以摄像机拍摄的二维照片为基准建立的坐标系。
读者也许已经发现了，如图4.1所示相机拍摄出来的图片都是以像素的形式储存的，由于存储顺序的原因，拍摄出来的坐标系的原点并不在图像的中心，这并不方便我们后续的建模，所以我们需要将坐标原点在左上角的（u，v）形式的图像坐标系转换为坐标原点在中心的（x，y）形式的图像坐标系。
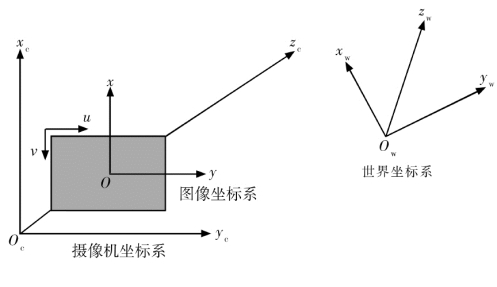
图4.1 坐标系之间的关系
显然，（x，y）与（u，v）存在如下转换关系：
其中，d x 代表x 轴方向一个像素的宽度，d y代表y轴方向上一个像素的宽度。d x，d y为摄像机的内参数。（u 0，v 0）是图像平面的主点，位于摄像机光轴与成像平面的焦点O′处，也是摄像机的内参数。
根据式（4-1）和（4-2），我们可以写出式（4-3）这个矩阵形式：
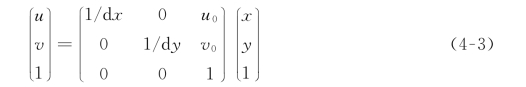
接着我们试图走出图像坐标系，将图像坐标系与相机坐标系连接起来。在这里，我们先假设主点就是成像仪的中心（实际上芯片的中心通常不在光轴上，这是因为我们无法对成像仪进行微米级别的精度安装，在后面的内容中我们将考虑这个误差），然后我们可以利用小孔成像的经典模型进行建模，如图4.2所示。
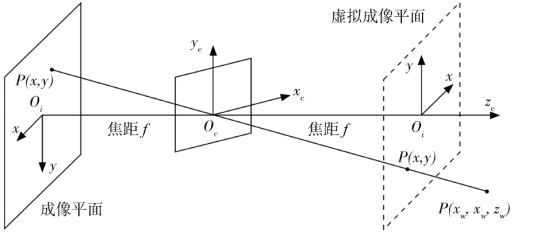
图4.2 小孔成像模型
这里为了将模型简化，将成像平面放在了小孔前面，形成了如图4.3的模型。在数学上这两个模型是等价的，并且后者更方便我们建模。
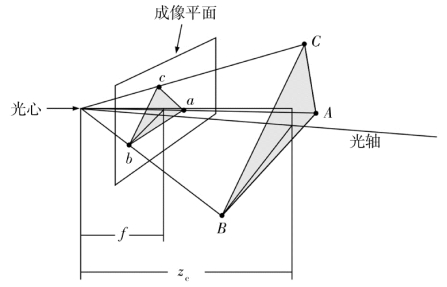
图4.3 透视投影模型
不妨设在相机坐标系上的一点为（x c，y c，z c），图像平面上所对应的一点为（x，y），我们可以很容易地写出如下公式：
显然，我们可以根据式（4-4）和（4-5）写出式（4-6）这个矩阵形式：
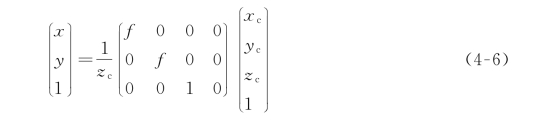
至此也就完成了图像坐标系与相机坐标系的联系。接下来，只剩下最后一步就可以将图像坐标系与世界坐标系联系起来。如图4.1所示，我们可以看到相机坐标系与世界坐标系只差一个旋转和平移的过程。基于刚体变换的模型，我们写出式（4-7）：
基于上面讲的内容，我们可以得出如图4.4的结果。图像坐标系就是这样与世界坐标系联系在一起的。
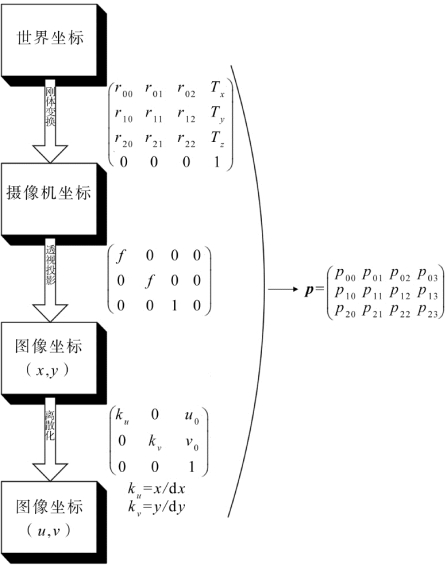
图4.4 图像坐标系与世界坐标系
之前的内容我们提到过主点并不是成像仪的中心，尽管可能误差并不大，但是我们仍然需要科学严谨地面对这些问题。其实只需在式（4-4）和（4-5）上作出一些修改，如式（4-8）和（4-9）所示。
其中c x 和c y 代表主点与成像仪中心的可能的偏移，写成矩阵形式如下：
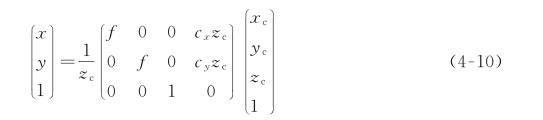
尽管这样的偏移是客观存在的，但是由于这只是建模的过程，这样的误差是可以容忍的。
综合式（4-3）（4-6）和（4-7），我们可以写出式（4-11）。
因为标定物是平面，所以我们可以把世界坐标系构造在z w ＝0的平面上。那么式（4-11）可以改写成式（4-12）。
得出上述式子我们就可以开始标定的过程了。从式（4-14），我们可以得出如下结论：我们只需要已知四个点在图像坐标系和世界坐标系的位置，就可以求出单应性矩阵H。
为了方便后续推导作以下运算：
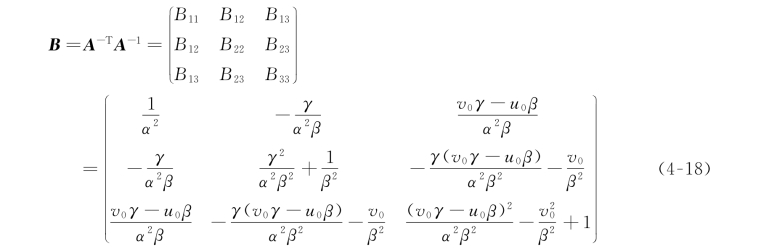
定义：
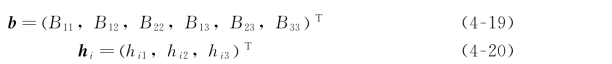
那么，我们有
其中
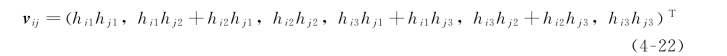
结合式（4-16）和式（4-17），我们得出：
根据式（4-23），我们发现只需要三幅图，就可以求出B 矩阵，再使用Cholesky分解，就可以轻松地得到摄像机的内参矩阵A。内参矩阵求出来了，外参矩阵自然也求出来了，这是由于A 是可逆矩阵。
尽管只需要三幅图与四个点我们就可以求出内参与外参矩阵，但是为了让求出的结果更鲁棒，我们更倾向于使用棋盘格的标定板，在这上面将会有许多可以检测到的特征点，并且我们会多次移动相机或标定板，每移动一次获取一幅新的图像。最后通过最小化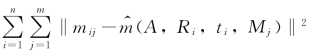
来获取内参矩阵和外参矩阵，通过这样的方法我们可以使得求出的结果不再只是拘泥于物理模型，而是具有了真正的实际物理意义。