7.3.2　连杆间的速度传递

7.3.2　连杆间的速度传递

操作臂是一个链式结构，每一个连杆的运动都与它的相邻杆有关。由于这种结构的特点，我们可以由基坐标系依次计算各连杆的速度。连杆i＋1的速度就是连杆i的速度加上附加到关节i＋1上的新的速度分量。

如图7.13所示，将机构的每一个连杆看作为一个刚体，可以用线速度矢量（v i）和角速度矢量（ωi）描述其运动。进一步，我们可以用连杆坐标系本身描述这些速度，而不用基坐标系。图7.14所示为连杆i和i＋1，以及在连杆坐标系中定义的速度矢量。当两个ω 矢量都相对于同一个坐标系时，连杆i＋1的角速度就等于连杆i的角速度加上一个由于关节i＋1的角速度引起的分量。参照坐标系｛i｝，上述关系可写成：

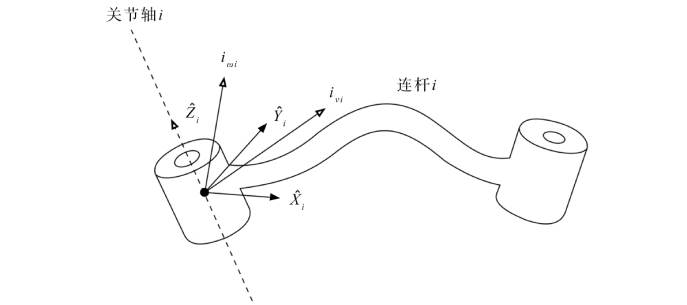
图7.13　连杆i的速度可以用矢量υi 和ωi 确定

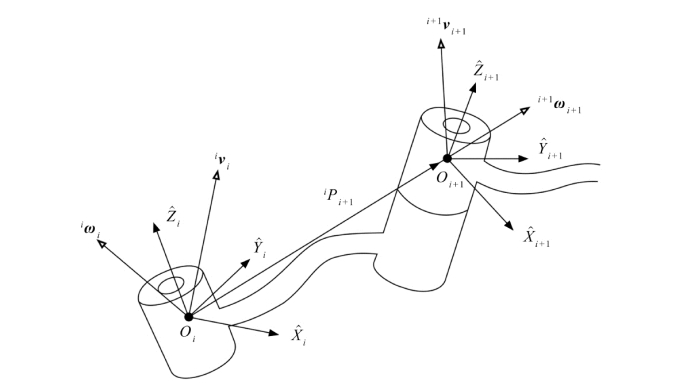
图7.14　相邻连杆的速度矢量

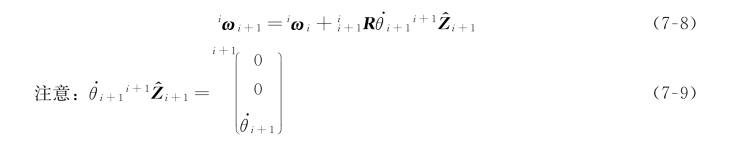
我们曾利用坐标系｛i｝与坐标系｛i＋1｝之间的旋转变换矩阵表达坐标系｛i｝中由关节运动引起的附加旋转分量。这个旋转矩阵绕关节i＋1的旋转轴进行旋转变换，变换为在坐标系｛i｝的描述后，这两个角速度分量才能相加。

在式（7-8）两边同时左乘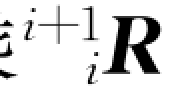，可以得到连杆i＋1的角速度相对于坐标系｛i＋1｝的表达式：

坐标系｛i＋1｝原点的线速度等于坐标系｛i｝原点的线速度加上一个由于连杆i的角速度引起的新的分量，有：

式（7-11）两边同时左乘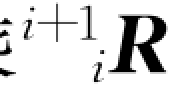，得：

对于关节i＋1为移动关节的情况，相应的关系为：

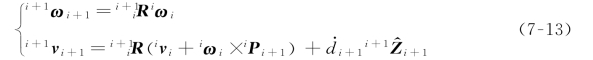
从一个连杆到下一个连杆依次应用这些公式，可以计算出最后一个连杆的角速度Nω 和线速度N v，注意，这两个速度是按照坐标系｛N｝表达的。在后面可以看到，这个结果是非常有用的。如果用基坐标系来表达角速度和线速度的话，就可以用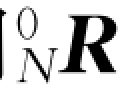 去左乘速度，向基坐标进行旋转变换。