8.3.3 基于图像的视觉伺服控制
IBVS的控制方式，主要依靠图像雅可比矩阵来解决摄像机与机器人之间的关系。图像雅可比矩阵建立的是机器人运动空间到图像特征平面之间的映射关系。图像雅可比矩阵由Weiss首先提出。
传统图像控制方案使用一组点的图像平面坐标来定义集合S，图像测量m 通常是图像点集的像素坐标（但是这不是唯一可能的选择）。在式子S＝S（m，α）中α为相机内在参数，其通过图像测量来表示像素特征。
1）交互矩阵。
更确切地说，在摄像机框架中带坐标的三维点的坐标向量X＝（x，y，z），它在图像中是X＝（x，y）形式的二维点坐标向量。所以我们可以得到：
m＝（u，v）为用像素单位来表示图像点的坐标；α＝（c u，c v，f，α）是一系列摄像头固有的内在参数：c u 和c v 是相机主点（即相机畸变中心），f 为相机焦距，α 是像素尺寸的比率。因此，图像平面点的坐标向量为s＝X＝（x，y），这种成像几何和立体投影技术在很多机器视觉相关书籍都有应用。对投影方程（8-24）求导，我们得到：
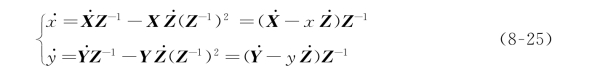
我们可以利用式（8-26）方程把三维点的速度与照相机空间速度联系起来：
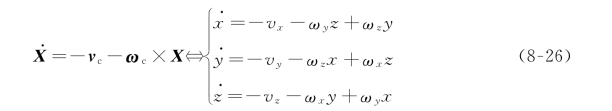
将式（8-24）代入式（8-25）得：
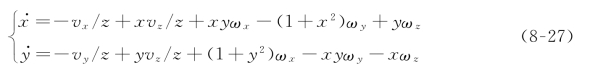
可以用
的形式来表示。
L x 是与x 相关的交互矩阵：
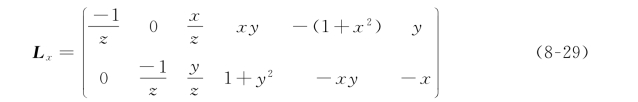
在矩阵L x 中，z值是与摄像机框架有关的点的深度，因此，任何使用这种相互作用矩阵的控制方案都必须要估计z 的值。同样地，摄像机内部参数涉及x 和y 的计算。
故L x 不能直接在（8-28）式中应用，必须使用近似值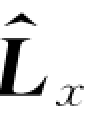
代替。
要控制6个自由度（即k≥6），至少需要三个点。如果我们使用特征向量X＝（x 1，x 2，x 3）叠加交互矩阵，我们得到三点：
这种情况下，将存在一些L x 是奇异的结构，此外还存在e＝0的4种不同的摄像机姿态。因为这些原因，更多情况下要考虑三点以上。
2）交互矩阵逼近。
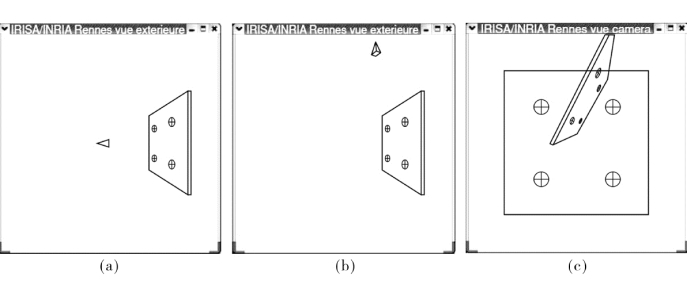
图8.6 定位相机能够在图像正中心观察到正方形
我们的目标是定位相机使得能够在图像正中心观察到正方形（如图8.6）。我们定义S 包括四个点的x 和y 的坐标，形成矩形。注意到，最初的摄像机姿态已经和期望的姿态有了很大的差距，尤其是基于图像的视觉伺服控制中最困难的旋转运动。在下面给出的模拟中，没有引入噪声或建模错误，以便在完美的条件下比较不同的行为。
选择
的结果如图8.7所示。
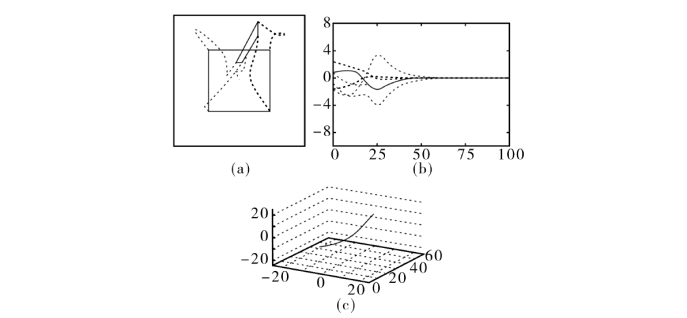
图8.7 估计式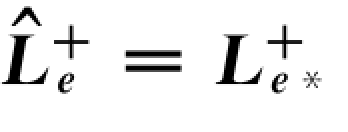
的控制方案
注意到尽管存在大位移，系统仍是收敛的。然而，计算的摄像机速度的组件和图像中的行为三维轨迹都未远离收敛的理想性质（例如，对于前30次左右的迭代）。
选择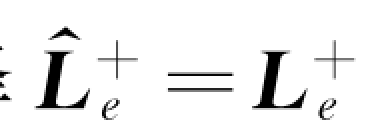
的结果显示如图8.8所示。
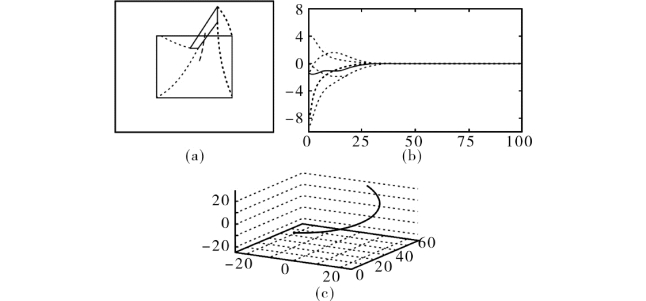
图8.8 估计式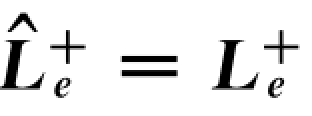
的控制方案
在这种情况下，点的轨迹在图像中几乎是直线，但在三维中的结果显示远不如
该选择下的情况令人满意。伺服系统表明相机的起始速度很快，故轨迹的起始端制约条件较多，并且摄像机的轨迹不是直线的。
而选择
在实践中表现出了良好的性能，如图8.9所示，可以看出摄像机的速度分量不包括大的振动，并且在图像和三维中为一条平滑的轨迹。
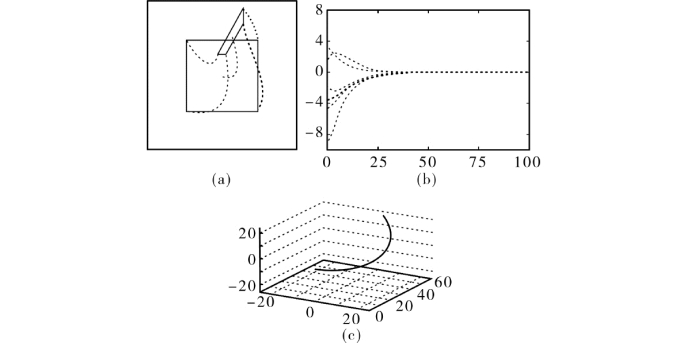
图8.9 估计式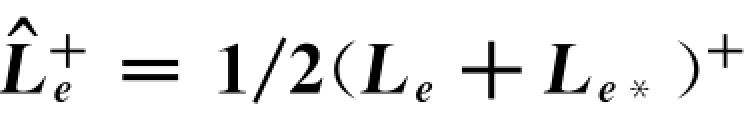
的控制方案