5.7.1 稀疏A* 与神经动力学融合算法
在旋翼无人机中应用,稀疏A* 与神经动力学融合算法的总体方案如下:首先建立基础环境模型空间,作为规划背景,本节融合算法的环境模型空间主要基于生物启发神经动力学模型而建立;然后在此环境模型之上引入改进的稀疏A* 算法,进而实现它们两者的融合。
该融合算法主要包括以下几个方面:
采用稀疏A* 算法:包括改进的经典A* 代价函数、改进的稀疏A* 约束条件、改进的稀疏A* 算法流程。
采用生物启发神经动力学模型算法:采用裁剪了航向后方神经元节点的改进的决策过程的生物启发神经动力学模型。
实现A* 代价函数与神经元活性值状态方程的融合:将稀疏A* 算法代价函数加入神经元活性值动态更新状态方程中,作为其代价评估因子。
实现稀疏A* 算法与神经元活性值状态更新过程的融合:将改进的A* 代价函数作为神经元活性值更新的启发项,用于引导活性值的选择性局部更新,摒弃传统的无条件全局更新方式。
1)A* 代价函数与神经元活性值状态方程的融合。
A* 代价函数与神经元活性值状态方程的融合即两者数学模型的融合。
已知经典生物启发神经动力学模型的神经元活性值的动态更新状态方程如式(5-28)所示,这是神经元活性值状态方程的初始形式,它表示规划空间中的任一神经元i随时间t变化的活性值状态为x i。将A* 代价函数融入式(5-28)中,将该初始的神经元活性值状态方程改进成如式(5-31)所示的形式。
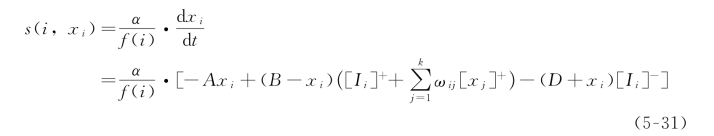 (https://www.daowen.com)
(https://www.daowen.com)
生物启发神经动力学模型的航迹决策规则与A* 算法的航迹决策规则在数值取向上恰好大小相反:神经动力学模型的航迹决策规则是以拥有最大活性值的神经元作为每一步决策所选择的对象,而A* 算法的航迹决策规则则是以拥有最小代价值的节点作为每一步决策所选择的对象。因此,在进行它们的数学模型的融合时,应充分考虑f(i)与![]() 的大小取向关系。
的大小取向关系。
2)稀疏A* 与神经动力学融合算法的航迹规划规划流程。
运用稀疏A* 与神经动力学融合算法对旋翼无人机进行航迹规划,其规划流程如图5.20所示。
3)稀疏A* 与神经动力学融合算法的航迹规划仿真实例。
现已知全局环境,并假设以下几点:飞行运动的起始点和目标点的位置固定不变;无人机是任务空间中的一个无体积的质点;无人机匀速飞行。现建立如下三维任务空间环境:在大小为65×65×30的三维坐标系中,设置错落有致的5座山峰,它们峰顶位置坐标分别为(10,10,15)、(15,55,15)、(20,35,20)、(35,50,20)、(40,25,25)。在此环境中,定义起始点的坐标为(3,62,11),目标点的坐标为(64,10,8),起始点、目标点和无人机各占据一个坐标点位置。如表5-3所示α 取不同值时在静态多峰山地环境下的航迹规划性能对比。
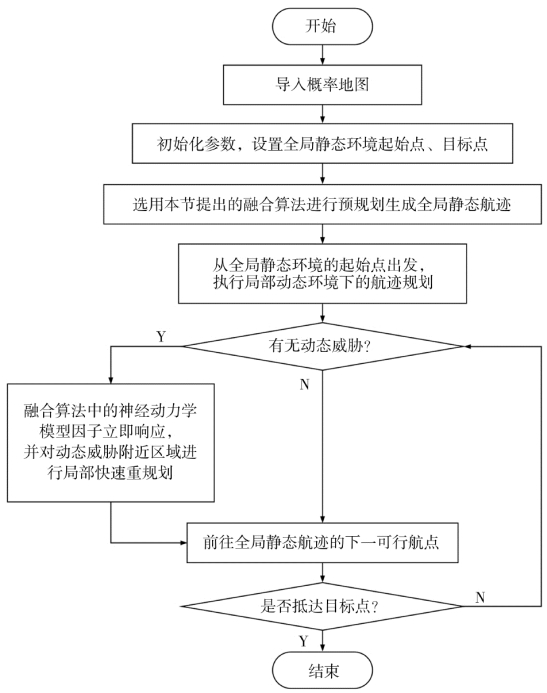
图5.20 稀疏A* 与神经动力学融合算法航迹规划流程图
表5-4 α取不同值时融合算法在静态多峰山地环境下的航迹规划性能对比
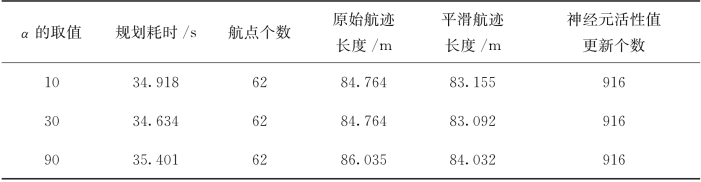
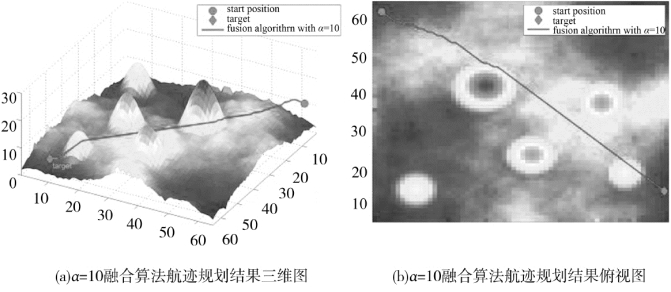
图5.21 融合算法航迹规划结果展示
稀疏A* 与神经动力学融合算法高时效的在线规划功能的实现,得益于其中的生物启发神经动力学模型对局部航迹的快速决策和调整能力。基于该融合算法环境建模中的神经动力学模型的最小神经元单元,就可以对实时获得的局部动态环境信息进行快速的建模处理,然后再根据这些神经元活性值抑制量的大小,来进行在线快速决策、调整局部航线,以实现旋翼无人机的在线避障功能。就这样,整体融合算法兼备了高时效和最优化的特点,从而具有集高效和优化于一身的在线规划能力。
