3.3.2 梯度下降法
梯度下降法(gradient descent)是一个一阶最优化算法,通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值,必须沿函数当前点对应梯度(或者是近似梯度)的反方向按规定步长进行迭代搜索。如果相反地向梯度正方向进行迭代搜索,则会接近函数的局部极大值点,这个过程则被称为梯度上升法。
在互补滤波法中,我们使用加速度计来补偿陀螺仪,将两者的数据融合解算出四元数下的姿态。在梯度下降法中,依然是通过加速度计的数据来与陀螺仪的数据进行融合。而不同点是:互补滤波法中,对载体坐标系b下的加速度做叉积以求出误差,补偿给陀螺仪以校正误差;梯度下降法中,通过加速度计的数据求出一组四元数q ,然后通过四元数的微分方程,并使用陀螺仪得到的数据求解出另外一组四元数qῶ。因为在高速运动状态下,陀螺仪数据更可靠;而在低速运动状态下,加速度计数据更可靠,所以两组四元数分别乘以权重再相加,就得到了期望的输出结果。
使用梯度下降法求解姿态的算法介绍:假设一个误差函数ef(x),我们希望其满足:ef(x)=0,即误差为0。接着,我们要求解这个方程,得到x 的值。此时x 值对应最优解。使用梯度下降法求解,首先我们就需要先求出它的导数![]() 将x 换成四元数Q=(q 0,q 1,q 2,q 3)。函数也相应变化,其导数变为如下形式:
将x 换成四元数Q=(q 0,q 1,q 2,q 3)。函数也相应变化,其导数变为如下形式:
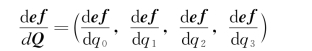
因为我们求解的姿态是三维姿态,而上式的因变量只对应了一维的情况。所以将因变量推广到xyz 轴下,变成一个多元向量函数:
求它的导数:
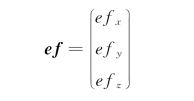
 (https://www.daowen.com)
(https://www.daowen.com)
当这个误差函数为0(即最小值)时,我们认为旋转矩阵没有误差,姿态是精确的。那么,接下来的任务就是使用前面介绍的梯度下降法相关公式来求解了。用前面阐述的方法求这个多元向量函数的导数(即它的雅可比矩阵):
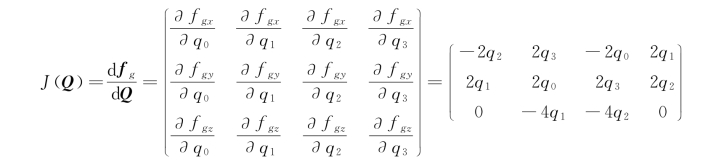
代入公式求出梯度:

通过离散叠加替代积分可以求解出一组四元数x n,将其乘以权重与陀螺仪数据通过四元数微分方程求解得到的另一组四元数qῶ。最终的公式为:
![]()
其中q g 为最终输出的四元数,α 为权重,q 为加速度计的数据通过梯度下降法得到的四元数,qῶ 为陀螺仪的数据通过四元数微分方程求解得到的四元数。
