7.6.3 李雅普诺夫稳定性分析
对于非线性系统，利用完备的基于模型的非线性控制器进行解耦和线性化，这种分析方法同样有效，因为最后得到的系统仍是线性的。但是，当控制器没有进行解耦和线性化，或解耦和线性化不完全或不精确时，整个闭环系统仍然是非线性的。对于非线性系统，稳定性和性能分析要困难得多。在本节，我们介绍一种对线性和非线性系统都适用的稳定性分析方法。
以简单的有摩擦质量弹簧系统为例，其运动方程为：
系统的总能量为：
式（7-135）中等号右边第一项为质量块的动能，第二项为储存在弹簧中的势能。注意，系统能量E 总是非负的。将式（7-135）对时间求导得到总能量的变化率：
则：
因此，通过能量分析可知，式（7-134）所示的系统在任何初始条件下，最终都将稳定在平衡点。这种基于能量分析的稳定性证明方法是一种一般方法的简单例子，这个一般方法是以19世纪的俄国数学家李雅普诺夫的名字命名的，称为李雅普诺夫方法。
这种稳定性分析方法的一个显著特点是不需要求解控制系统的微分方程即可判断系统的稳定性。然而，虽然李雅普诺夫方法可以判断稳定性，但它通常无法提供任何有关瞬时响应或系统性能的信息。注意，这种能量分析方法不能给出系统是过阻尼或欠阻尼的信息，也不能给出系统抑制干扰所需要的时间。稳定性和动态性能的主要区别在于：虽然系统是稳定的，但它的控制性能可能并不令人满意。
李雅普诺夫方法比前述的例子更具一般性。它是为数不多的几种能够直接应用到非线性系统上的稳定性分析方法之一。为了很快了解李雅普诺夫方法，我们将简单介绍一下这个理论。
李雅普诺夫方法用于确定下列微分方程的稳定性：
其中，X 为m×1矢量，f（·）可以是非线性函数。注意，高阶微分方程总是可以被写成一组形式为式（7-140）的一阶微分方程。为了用李雅普诺夫方法证明一个系统是否稳定，必须构造一个具有如下性质的广义能量函数υ（ X）：
（1）υ（ X）具有连续的一阶偏导数，对于任意X 有υ（ X）＞0，且υ（ 0）＝0除外。
（2）
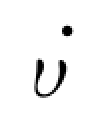（X）≤0，
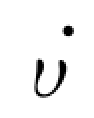（X）指υ（ X）在系统所有轨迹上的变化率。
若这些性质仅在特定区域成立，则相应的系统为弱稳定的；若这些性质在全局成立，则相应的系统为强稳定的。可直观解释为，一个正定的“能量形式”的状态函数，其值是一直减小的或保持为常数，则系统是稳定的，即系统的状态矢量是有界的。
若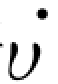
（X）严格小于零，则系统的状态是渐进收敛于零矢量。LaSalle和Lefschetz对李雅普诺夫最初的工作进行了重要发展，他们指出，在一定情况下，即使当
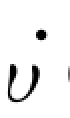（X）≤0，系统也是渐进稳定的。为此，可以通过稳定分析讨论
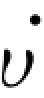（X）＝0的情况，以便确定这个系统是渐进稳定的还是位于υ（ X）＝0以外的某处。
式（7-140）所描述的系统称为自治系统，因为函数f（·）不是时间的显函数。李雅普诺夫方法也可以推广到非自治系统中去，其中时间是非线性函数的自变量。