7.3.5　速度和静力的笛卡尔变换

7.3.5　速度和静力的笛卡尔变换

可以根据6×1维的刚体广义速度表达式进行讨论：

同样，考虑6×1维的广义力矢量表达式，则：

其中F 是一个3×1的力矢量，N 是一个3×1的力矩矢量。很自然地可以想到用6×6变换矩阵将这些量从一个坐标系映射到另一个坐标系。这些工作已在连杆之间速度和力的传递讨论中做过。这里，用矩阵算子的形式写出式（7-10）和式（7-12），将坐标系｛A｝中的广义速度矢量变换为在坐标系｛B｝中的描述。

这里涉及的两个坐标系之间的连接是刚性的，所以在推导关系式时式（7-10）中出现的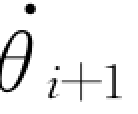被置成0。

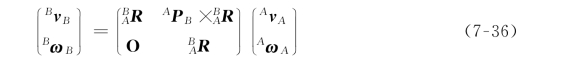
式中，叉乘可看成是矩阵算子：

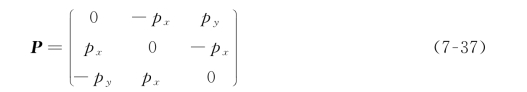
现在，式（7-36）将一个坐标系的速度与另一个坐标系的速度联系起来，因此这个6×6算子被称为速度变换矩阵，用符号T v 表示。在这种情况中，它是一个将｛A｝中的速度映射到｛B｝中的速度的速度变换，所以可用式（7-38）将式（7-36）表示成紧凑的形式：

已知｛B｝中的速度值，为了计算在｛A｝中的速度描述，可以对式（7-36）求逆：

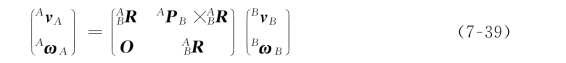
则：

注意从坐标系｛B｝到坐标系｛A｝的速度变换是由（或它的逆变换）确定的，并且应被看作是瞬时结果。同样，由式（7-31）和式（7-35）可得6×6的矩阵，它可将在坐标系｛B｝中描述的广义逆矢量变换成在坐标系｛A｝中的描述，即为：

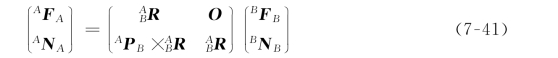
可以写成紧凑形式：

其中，T f 表示一个力－力矩变换。

速度和力变换矩阵与雅可比矩阵相似，可以把不同坐标系中的速度和力联系起来。参照雅可比矩阵，有

可通过式（7-41）和式（7-39）对式（7-43）进行检验。