8.3.4 基于视觉伺服控制的带臂旋翼无人机
旋翼飞行机械臂系统的主要工作环境是具有复杂干扰的非结构三维空间，同时自身的耦合特性对伺服控制造成了极大的局限性。所以采用混合视觉伺服的方法，可以在强干扰环境下保持良好的全局收敛性；特别是当机体起飞初始位置离期望目标点较远时，依然能够保持目标识别点始终位于相机图像平面内。
针对传统的基于图像与基于位置的视觉伺服的缺陷以及系统自身欠驱动等问题，建立了运动学模型和提出了基于力平衡原理的动力学联合建模，并通过欧几里得单应性矩阵分解设计出旋翼飞行机械臂系统的混合视觉伺服控制方法，在图像空间控制平移、笛卡尔空间控制旋转，减弱了平移与旋转之间的相互影响实现解耦效果，改善了系统对非结构因素的抗扰性能和全局稳定性。
1）欧几里得充分扩解。
假设在平面μ 中存在一个由四个圆点组成的三维目标点P 0，如图8.10所示，可以得到该目标点在当前机载相机平面F 和期望机载相机平面F* 上的映射点P 0 和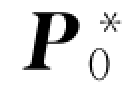
。它们之间的关系可以通过一个非奇异的3×3的矩阵H 表示为：
其中，矩阵H 称为平面单应性矩阵。
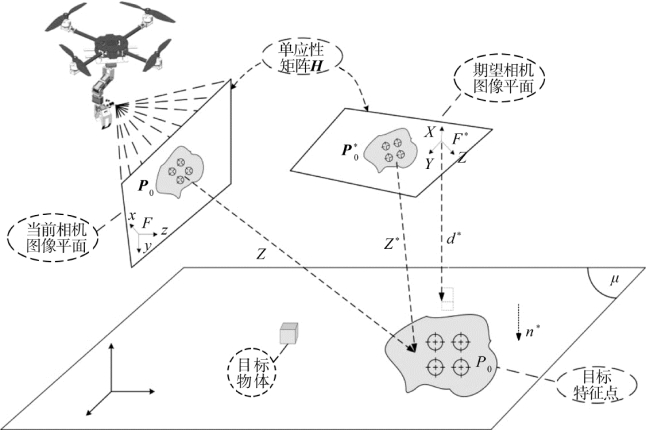
图8.10 UAM 混合视觉伺服原理图
由旋翼飞行机械臂末端机载相机的内在参数矩阵为K，可知：
假设该相机已经标定，即参数矩阵K 已知，则欧几里得单应性矩阵H E 和平面单应性矩阵H 之间的关系可表示为：
可将其分解为一个旋转矩阵R 和一个秩为1的矩阵：
而且，目标点到相机未知的深度信息Z 与d* 之间的比率可通过下式计算得到：
最后，也可以得到：
这些参数的得到对我们接下来设计的混合视觉伺服控制方法是十分重要的。
2）机械臂控制器设计。
为了能够得到机载相机的运动速度，进而间接控制旋翼飞行机械臂系统向指定目标伺服运动，通常要三维估计旋转矩阵（即得到一个特征矩阵），这里用μ 表示旋转轴、θ表示从矩阵R 中提取得到的相对应旋转轴的旋转角度。相比较不同于经典的表示方法μsinθ和μsin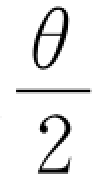
的是向量μθ表示法使得整个工作空间不存在奇点。μθ的一阶导数可以表示为机载相机速度ν＝（v TωT）T 的相关函数：
其中，雅可比矩阵Lω（u，θ）可以由下式得到：
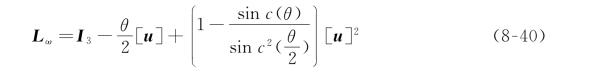
这里sin c（θ）＝sinθ/θ，[u]是与向量u相关的反对称矩阵。雅可比矩阵Lω 的行列式为：
当θ＝2kπ时，∀k ∈Z*，它是唯一的。同时当θ 取值极小时，Lω 约等于I 3。
接下来我们考虑位置控制向量，如图8.11所示，在平面μ 中存在目标特征点ρ0，其坐标向量m ＝（X，Y，Z）T 的导数在当前相机平面中表示为：
定义图像扩充坐标m e 如下：
这里，z＝log Z 表示标准坐标，图像扩充坐标m e 的导数推导如下：
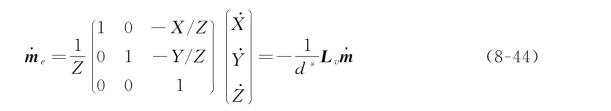
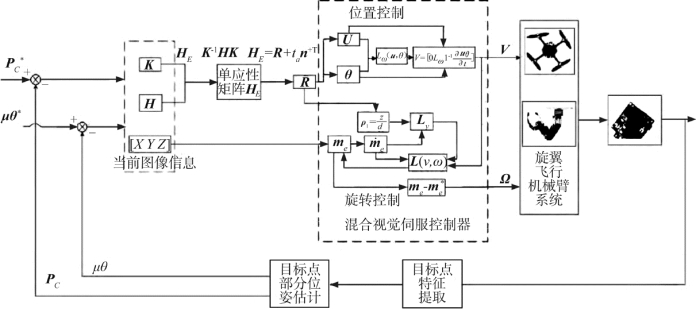
图8.11 混合视觉伺服控制算法原理
而深度信息d* 是未知的，由式（8-37）中比率ρ1 可知上三角矩阵L v 为：
最后，根据式（8-42）和式（8-44）可以推导出：
其中，矩阵L（v，ω）表示为：
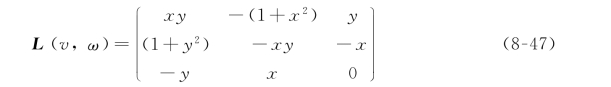
简而言之，系统混合伺服任务可以描述为以下误差函数ε 趋近于零：
其中，（m e－m e*）T 可以直接由当前图像平面和期望图像平面得到；θu T 可以直接由公式8-38间接得到，约等于logρ2；误差函数ε的导数和机载相机的速度之间的函数关系是：
同样的，根据公式（8-39）和（8-46）可以得到矩阵L，是一个上三角矩阵：
当且仅当相机光学中心处于平面μ 上时，该矩阵才是奇异的。
综上，图像坐标m e指数收敛于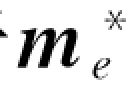
以及μθ指数趋近于0，都可以通过
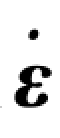＝－λε调整它们的收敛速度，尤其是针对被抓取的地面固定目标而言，再联立式（8-49）可得到：
最终，机载相机的速度转换成机械臂各关节速度和飞行器的运动，以达到控制整个系统的目的，然而L－1 只是近似值，因为矩阵L取决于d* 的准确度，所以要对d* 初始值进行近似估计，这样会对系统前期稳定性造成轻微的影响，系统完整的控制律可表示为：
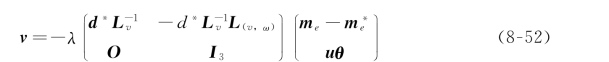
由于当θ 取值极小时，Lω 约等于I 3，所以这里令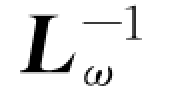
≈I 3。
图8.12给出了混合视觉伺服方法的控制框图。矩阵L－1是一个上三角矩阵，在整个工作空间中不存在奇点，这对于旋翼飞行机械臂系统的强耦合特性而言，能使相机在笛卡尔空间具有较光滑的运动轨迹，若能完整地得到目标位姿，则无论起飞的初始位置在何处，系统总是能够保证目标特征点始终保持在相机视野范围内，并能够保持全局收敛性。
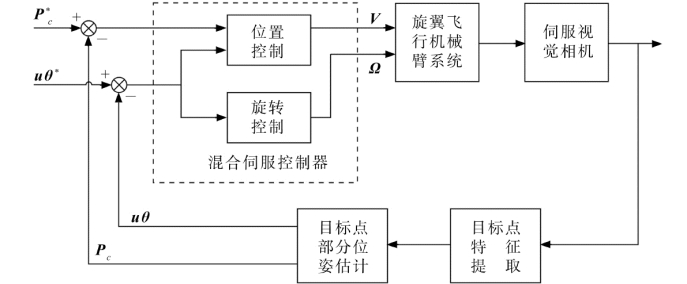
图8.12 UAM 混合视觉伺服控制器框图