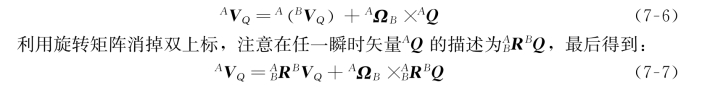7.3.1 刚体的线速度和角速度
1）线速度。
把坐标系｛B｝固连在一刚体上，要求描述相对于坐标系｛A｝的运动BQ，如图7.10所示。这里已经认为坐标系｛A｝是固定的。
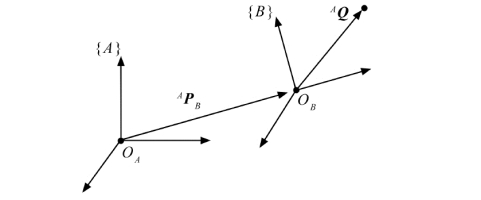
图7.10 坐标系｛B｝以速度AVBorg 相对于坐标系｛A｝平移
坐标系｛B｝相对于坐标系｛A｝的位置用位置矢量A P B 和旋转矩阵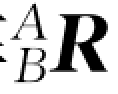
来描述。此时，假定方位
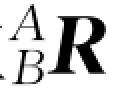不随时间变化，则Q 点相对于坐标系｛A｝的运动是由于A P B 或B Q 随时间的变化引起的。
求解坐标系｛A｝中Q 点的线速度是非常简单的。只要写出坐标系｛A｝中的两个速度分量，求其和为：
式（7-2）只适用于坐标系｛B｝和坐标系｛A｝的相对方位保持不变的情况。
2）角速度。
现在讨论两坐标系的原点重合、相对线速度为零的情况，而且它们的原点始终保持重合。其中一个或这两个坐标系固连在刚体上，但是为清楚起见，图7.11没有表示出刚体。
坐标系｛B｝相对于坐标系｛A｝的方位是随时间变化的。如图7.11所示，｛B｝相对于｛A｝的旋转速度用矢量AΩB 来表示。已知矢量B Q 确定了坐标系｛B｝中一个固定点的位置。现在，考虑最重要的问题：从坐标系｛A｝看固定在坐标系｛B｝中的矢量，这个矢量将如何随时间变化？ 这个系统是否转动？
假设从坐标系｛B｝看矢量Q 是不变的，则：
既然它相对于｛B｝不变，显然从坐标系｛A｝中看出点Q 的速度为旋转角速度AΩB。求点Q 的速度，可用一个直观的方法。图7.12所示为两个瞬间量表示矢量Q 绕AΩB 的旋转。这是从坐标系｛A｝中观测到的。
由图7.12，可以计算出这个从坐标系｛A｝中观测到的矢量的方向和大小的变化。第一，显然微分增量ΔQ 一定垂直于AΩB 和Q；第二，从图7.12可以看出微分增量的大小为：
有了大小和方向这些条件，即可得到矢量积。实际上，这些矢量的大小和方向满足下面算式：
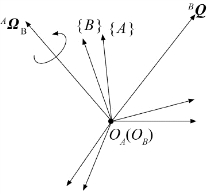
图7.11 固定在坐标系｛B｝中的矢量BQ 以角速度AΩB相对于坐标系｛A｝旋转
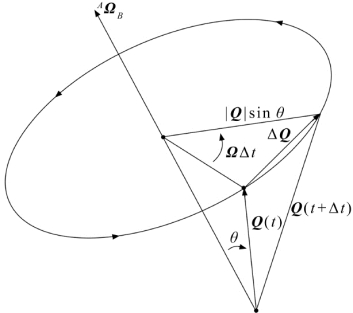
图7.12 用角速度表示的点的速度
在一般情况下，矢量Q 是相对于坐标系｛B｝变化的，因此要加上此分量，得：
