5.3.2 SLAM 问题的一般模型
由于机器人受到控制噪声和传感器噪声的干扰,可以将控制量U 和传感器采集的数据Z 作为对机器人位置的约束,由于噪声的存在,如果仅仅用一方面的数据(仅用U 或Z)来进行约束,那么随着时间推移,对误差的积分会越来越大,从而导致定位失败,可以通过U,Z,机器人的位置三者之间的约束关系来消除误差积分带来的影响。实验刚开始时,这三者之间的约束关系很弱,随着实验的继续进行,机器人在环境中观测到的特征越来越多,有些特征被反复多次地观测到,三者之间的约束性质越来越强,经过多次实验,这种约束关系最终不再变化,稳定下来,机器人将能够准确地在环境中定位。
为了解决SLAM 问题,需要了解以下信息和基本概念:
(1)机器人路径给定为:X T ={x 0,x 1,x 2,…,x T}。
(2)本体感受传感器数据的序列:U T ={u 0,u 1,u 2,…,u T}。
(3)外感受式传感器的测量序列:Z T ={z 0,z 1,z 2,…,z T}。
(4)信任度的分布。一般来说,机器人不能直接测量自身的真实位置和姿态,所以,机器人的状态只能由数据推测。有关机器人状态的最好猜测,叫信任度。在概率机器人学中,信任度通过条件概率分布来表示(如图5.6所示),因此是以可用数据为条件的状态变量后验概率。如果把状态x i 的信任度用bel(x i)来表示,有:bel(x i)=p(x t∣z 1→t,u 1→t)
式中,后验概率p(x t∣z 1→t,u 1→t)表示给定所有的后观测z 1→t 和所有过去控制输入u 1→t,机器人处在x i 的概率。
正好在控制输入u t 之后,融合新的观测值z t,形成一个后验可以写成:![]()
(5)环境地图的给定:M ={m 0,m 1,m 2,…,mn}。
(6)概率运动模型:x t=f(x t-1,u t)。
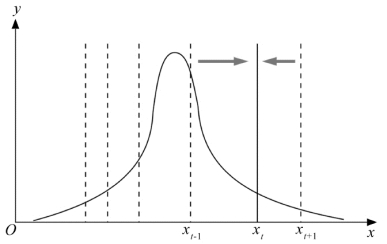
图5.6 路径概率分布图
(7)概率测量模型:z t=h(x t,M)。
(8)预测(动作)更新:
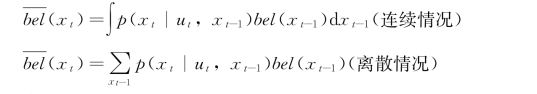 (https://www.daowen.com)
(https://www.daowen.com)
含义:
①bel(x t-1)表示图5.6中的凸峰曲线,表示上一次机器人位置的可信度的分布;
②p(x t∣u t,x t-1)表示机器人上一次的位置是x t-1,在读入编码器数据u t 后,新位置是x t 的概率;
③整体的含义是遍历整个x 轴,从所有位置移动到x t 的概率累加和;
(9)感知(测量)更新:
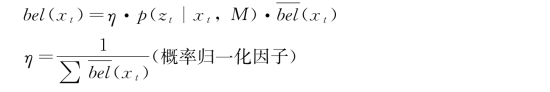
含义:
①bel(x t)表示在预测概率地图中x t 位置的信度值;
②p(z t∣x t,M)表示在x t 位置观测到z t 数据的概率。
SLAM 定位算法模型可以简述为:
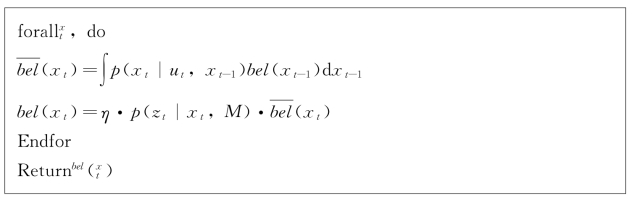
具体可以通过图5.7来表达SLAM 的基本框架。
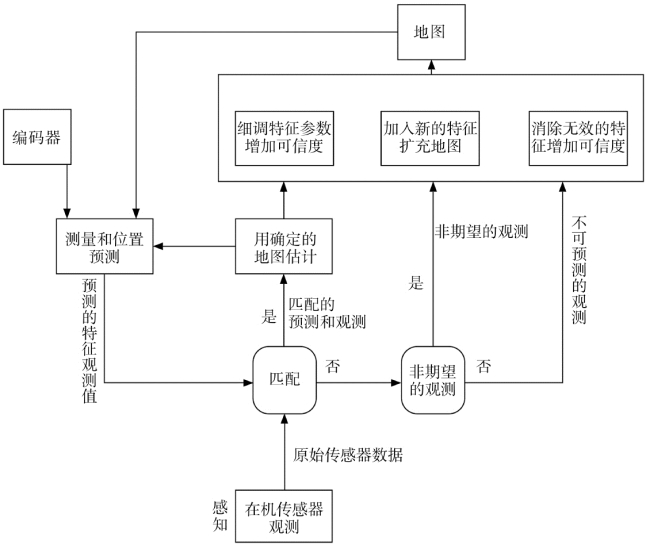
图5.7 SLAM 基本框架图
