1.3.2 连续转动
2026年01月15日
1.3.2 连续转动
空间中的旋转矩阵有3个自由度(见图1.16),要表达一般的旋转矩阵,可拆解成3次旋转角度,以对应到空间中的3个自由度。
Z-Y-X 欧拉角:
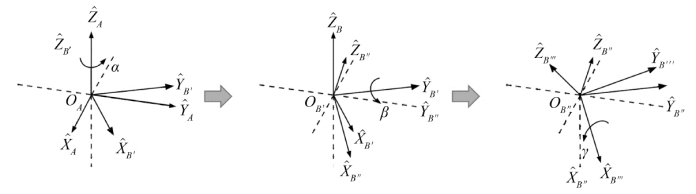
图1.16 旋转矩阵3个自由度
1)将坐标系{A}与坐标系{B}的原点重合。
2)将坐标系{A}绕着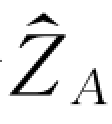 轴旋转α 角度,并把新的坐标系记为{B′ }。
轴旋转α 角度,并把新的坐标系记为{B′ }。
3)将坐标系{B′}绕着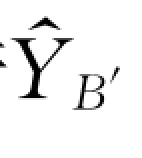 轴旋转β 角度,并把新的坐标系记为{B″ }。
轴旋转β 角度,并把新的坐标系记为{B″ }。
4)将坐标系{B″ }绕着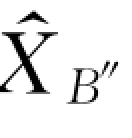 轴旋转γ 角度,新的坐标系记为{B‴ }, {B‴ }与{B}重合。
轴旋转γ 角度,新的坐标系记为{B‴ }, {B‴ }与{B}重合。

如果把这些旋转看成是坐标系的描述,就可写出:
![]()
根据Z-Y-X 欧拉角的定义,每个旋转矩阵都是绕着自身坐标系旋转的:
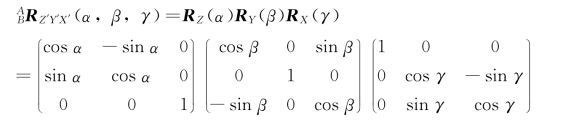 (https://www.daowen.com)
(https://www.daowen.com)
例1-4:以欧拉角方法旋转,先对X 轴旋转60°,后对Y 轴旋转30°,和先对Y 轴旋转30°,后对X 轴旋转60°各自的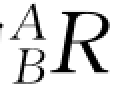 相同么?
相同么?
解:①先对X 轴旋转60°,后对Y 轴旋转30°:

②先对Y 轴旋转30°,后对X 轴旋转60°:
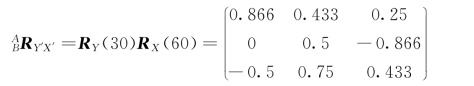
因此可发现两个旋转矩阵并不相同。这里要注意坐标轴旋转的次序,不同次序组合的欧拉角,将得到不同的旋转矩阵。
旋转矩阵反推旋转角度:
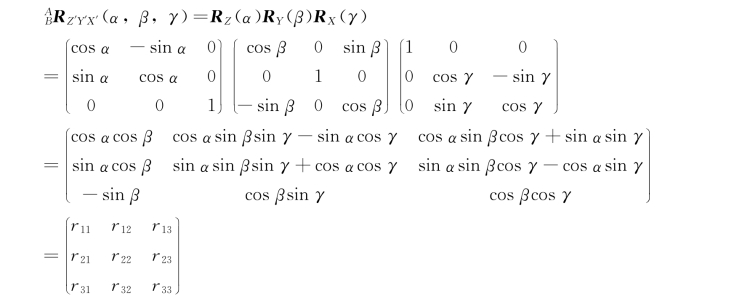
若β ≠±90°,可得到:

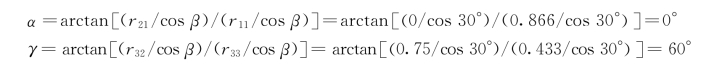
Z-Y-Z 欧拉角:

