7.4.1　加速度

7.4.1　加速度

同速度一样，当微分的参考坐标系为世界坐标系｛U｝时，可用下列符号表示刚体的速度：

1）线加速度。

式（7-7）描述了坐标系｛A｝下的速度矢量B Q，当坐标系｛A｝的原点与坐标系｛B｝的原点重合时，速度矢量B Q 可表示为：

等号左边描述的是矢量A Q 随时间变化的情况。由于两个坐标系的原点重合，因此可把式（7-48）改写成如下形式：

这种形式的方程在求解相应的加速度方程时很方便。

对式（7-48）求导，当坐标系｛A｝和｛B｝的原点重合时，可得到B Q 的加速度在坐标系｛A｝中的表达式：

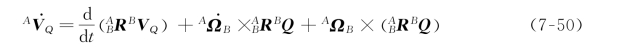
对式（7-50）等号右边的第一项和最后一项应用式（7-49），则可化为：

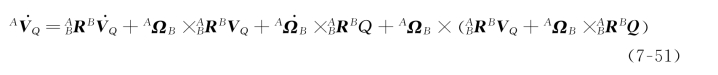
将式（7-51）的同类项合并，整理得：

最后，为了将结论推广到两个坐标系原点不重合的一般情况，我们附加一个表示坐标系｛B｝原点线加速度的项，最终得到一般表达式：

值得指出的是当B Q 是常量时，则：

在这种情况下，式（7-53）简化为：

式（7-55）常用于计算旋转关节操作臂连杆的线加速度。当操作臂的连接为移动关节时，常用一般表达式（7-53）。

2）角加速度。

假设坐标系｛B｝以角速度AΩB 相对于坐标系｛A｝转动，同时坐标系｛C｝以角速度BΩC 相对于坐标系｛B｝转动。为求AΩC，在坐标系｛A｝中进行矢量相加：

对式（7-56）求导，得：

将式（7-49）带入式（7-57）中，得：

式（7-58）用于计算操作臂连杆的角加速度。