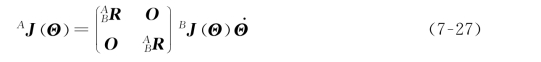7.3.3 雅可比矩阵
雅可比矩阵是多元形式的导数。例如，假设有6个函数，每个函数都有6个独立的变量：
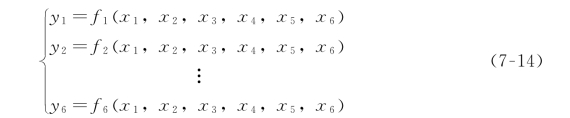
也可以用矢量符号表示这些等式：
现在，如果想要计算出y i 的微分关于x i 的微分的函数，可简单应用多元函数求导法则计算，得到：
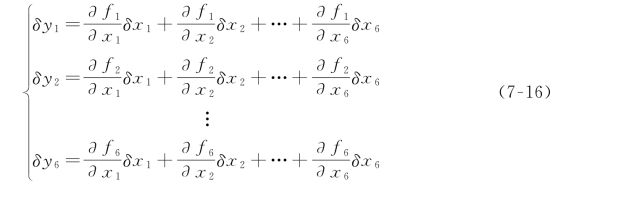
将式（7-16）写成更为简单的矢量表达式：
式（7-16）中的6×6偏导数矩阵就是我们所说的雅可比矩阵J。注意，如果f 1 （X）到f 6 （X）都是非线性函数，那么这些偏导数都是x i 的函数，因此可以表示如下：
将上式两端同时除以时间的微分，可以将雅可比矩阵看成是X 中的速度向Y中速度的映射：
在任一瞬时，X 都有一确定的值，J（ X）是个线性变换。在每一个新时刻，如果X改变，线性变换也会随之而变。所以，雅可比是时变的线性变换。
在机器人学中，通常使用雅可比矩阵将关节速度与操作臂末端的笛卡尔速度联系起来，比如：
其中，Θ 是操作臂关节角矢量，ν 是笛卡尔速度矢量。在式（7-20）中，我们给雅可比表达式附加了左上标，以此表示笛卡尔速度所参考的坐标系。当参考坐标系很明显，或者对后续推导并不重要时，这个左上标就可以略去。注意到，对于任意已知的操作臂位形，关节速度和操作臂末端速度的关系是线性的，然而这种线性关系仅是瞬时的，因为在下一刻，雅可比矩阵就会有微小的变化。对于通常的6关节机器人，雅可比矩阵是6×6阶的矩阵，
是6×1维的，0ν也是6×1维的。这个6×1笛卡尔速度矢量是由一个3×1的线速度矢量和一个3×1的角速度矢量组合起来的：
可以定义任何维数的雅可比矩阵（包括非方阵形式）。雅可比矩阵的行数等于操作臂在笛卡尔空间的自由度数量，雅可比矩阵的列数等于操作臂的关节数量。例如，对于平面操作臂，虽然雅可比矩阵不能超过3行，但对于冗余度平面操作臂，可以有任意多个列（列数和关节数相等）。
对于两连杆的操作臂，可以写出一个2×2的雅可比矩阵，该矩阵将关节速度和末端执行器的速度联系起来。可以写出坐标系｛3｝中的雅可比表达式：
写出坐标系｛0｝中的雅可比表达式：
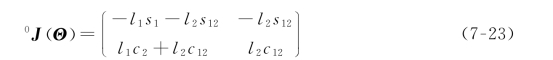
注意，在上述两种情况下，都选择了一个方阵将关节速度和末端执行器的速度联系起来。当然，也可以选择包含末端执行器角速度的3×2阶雅可比矩阵。
已知坐标系｛B｝中的雅可比矩阵：
我们关心的是给出雅可比矩阵在另一个坐标系｛A｝中的表达式。首先，注意到已知坐标系｛B｝中的笛卡尔速度矢量可以通过如下变化得到相对于坐标系｛A｝的表达式：
因此，可以得到：
显然，利用下列关系式可以完成雅可比矩阵参考坐标系的变换：
