7.4.4　机载操作臂动力学的拉格朗日公式

7.4.4　机载操作臂动力学的拉格朗日公式

替代牛顿-欧拉方法的另一种方法是本节我们将要简要介绍的拉格朗日动力学公式。牛顿-欧拉公式可以被认为是一种解决动力学问题的力平衡方法，而拉格朗日公式则是一种基于能量的动力学方法。当然，对于同一个操作臂来说，这两种方法得到的运动方程是相同的。

首先讨论操作臂动能的表达式。第i根连杆的动能k i 可以表示为：

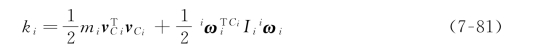
式（7-81）中等号右边第一项是由连杆重心线速度产生的动能，第二项是由连杆的角速度产生的动能。整个操作臂的动能是各个连杆动能之和：

实际上操作臂的质量矩阵一定是正定的，这类似于质量总是正数这一事实。

第i根连杆的势能u i 可以表示为：

其中，0g是3×1的重力矢量，0P Ci 是位于第i根连杆重心的矢量，u ref i 是使u i的最小值为零的常数。操作臂的总势能为各个连杆势能之和：

因为式（7-85）中的0P Ci 是Θ 的函数，由此可以看出操作臂的势能u（ Θ ）可以描述为关节位置的标量函数。

拉格朗日动力学公式给出了一种从标量函数推导动力学方程的方法，我们称这个标量函数为拉格朗日函数，即一个机械系统的动能和势能的差值。这里，操作臂的拉格朗日函数可表示为：

则操作臂的运动方程为：

这里τ 是n×1的驱动力矩矢量。对于操作臂来说，方程（6-88）变为：

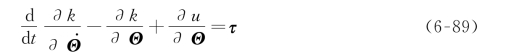
为简化起见，这里省略了k（·）和u（·）中的自变量。