3.2　系统可观性分析

3.2　系统可观性分析

图3.10　系统状态图

可观测性表示输出可以完全反映系统状态的特性，因此不仅要考虑系统的状态方程还要考虑输出方程。以考虑连续时间线性时变系统∑为例，其状态方程和输出方程分别为：

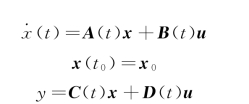
其中t，t 0 ∈J，x 为n维状态，u为p 维输入，y为q维输出，t 0 为初始时刻，A（t）为n×n维的系统矩阵，B（t）为n×p 维的输入矩阵，C（t）为q×n维的输出矩阵，D（t）为q×p 维的传输矩阵，A（t）的元在J 上为绝对可积，B（t）的元在J 上为平方可积。对系统的运动进行分析可知，系统∑状态解的表达式为：

其中φ（t，τ）为系统的状态转移矩阵，δ（t）为单位冲激函数。

在许多实际问题中，控制系统的状态变量不是由直接测量得到的，而是通过某种观测方法得到的，某种观测系统所得到的结果对系统状态真实性的反映就是系统的可观测性。可观性反映系统外部可直接或间接测量的输出y（t）和输入u（t）来确定或识别系统状态的能力。

如果系统的任何内部运动状态变化都可由系统的外部输出和输入唯一地确定，那么称系统是能观的，或者更确切地说，是状态能观的。否则，就称系统为状态不完全能观的。下面通过例子来说明可观性的意义。

例3-1：给出两个传感器GPS和加速度计，那么哪一个能够稳定地估计出多旋翼速度？

为了简化起见，我们用GPS观测位置，一般用如下模型：

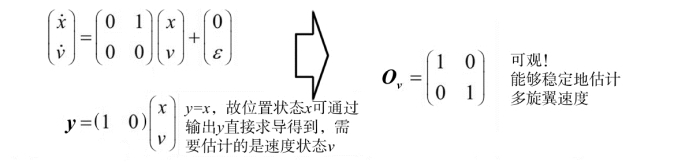
其中x，v ∈R分别表示位置状态和速度状态，ε ∈R表示已知统计特性的噪声。

为了简化起见，用加速度计估计速度，一般用如下模型：

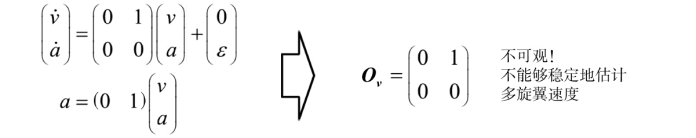
其中v，α ∈R分别表示速度大小和加速度大小，ε ∈R表示已知统计特性的噪声。