2.4 旋翼的空气动力学效应
当飞行器具有前飞的速度时,旋翼不仅会受到沿着构造旋转轴的升力F 和反扭矩Q的作用,同时还会受到阻力D 和侧倾力矩L 的作用。同时,升力F,反扭矩Q,阻力D以及侧倾力矩L 均与旋翼转速ω 的平方成比例关系,具体的表述见式(2-3):
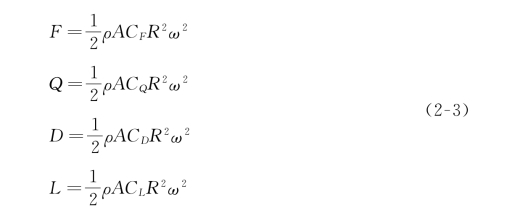
其中,CF 为旋翼的拉力系数,CQ 为旋翼的扭矩系数,CD 为旋翼的阻力系数,CL为旋翼的侧倾力矩系数,ρ,R,A 分别表示空气密度、旋翼桨叶半径以及桨盘的面积。可利用动量理论和叶素理论分别对相对气流和旋翼的几何特性进行分析,以准确求取旋翼的空气动力学系数。
1)诱导速度的计算。
诱导速度,可以反映出旋翼与其所处周围空气的相互作用,能够引起速度大小和方向变化。在旋翼改变空气的动量和动能的同时,气流对桨盘产生的反作用就形成了空气动力。
以飞行器处于悬停状态为例,推导诱导速度。如图2.7所示,飞行器处于悬停状态,旋翼的滑流截面积为上面大下面小的形状,其中V 0 代表旋翼处的空气速度,v 1 代表旋翼桨盘处的诱导速度且与该处的空气速度V 1 相等,v 2 代表旋翼下方很远处的诱导速度且与该处的空气的速度V 2 相等。根据动量定理,针对旋翼滑流,有:
![]()
其中,m′为单位时间内流过滑流任一截面的空气质量,F′为滑流所受到的合外力。根据质量守恒定律,可得:
![]()
其中ρ 为空气密度,V 0,V 1,V 2 为图2.7所示各区域的空气速度,S 0,S 1,S 2 为对应的区域截面积,C 为正常数。
因此,气流对旋翼桨盘产生的反作用力即为旋翼产生的升力F:
![]()
根据能量守恒定律和旋翼滑流的动能变化率可确定旋翼消耗的功率:
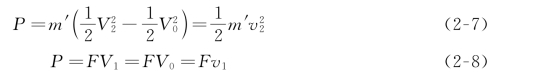
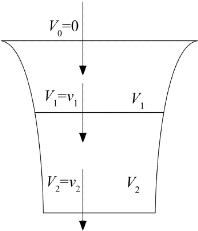
图2.7 诱导速度
根据式(2-6)(2-7)及(2-8)可得旋翼桨盘下方的诱导速度等于桨盘处的诱导速度的2倍,则:

因此式(2-6)表达的旋翼产生的升力可重新表达为:
![]()
其中,ρ 为空气密度,A 为旋翼桨的桨盘面积。根据式(2-10)可得飞行器处于悬停状态下的旋翼诱导速度为:

同理,利用动量理论和能量定理,可推导出飞行器以速度v 飞行时的诱导速度:(https://www.daowen.com)
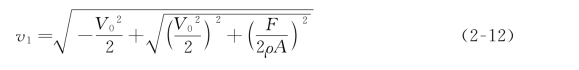
2)叶素理论。
叶素理论是假设旋翼气流无滑流收缩,将旋翼桨叶分成很多小的小段,即叶素,根据旋翼翼型可以对每个叶素上的空气动力进行计算,然后沿着径向进行积分求得旋翼的总的空气动力。叶素理论考虑了旋翼的几何特性和运动特性。
首先,取桨叶上径向位置为r,宽度为Δr,弦长为c的叶素,对其进行受力分析,如图2.8所示。其中θs 为桨叶叶素几何安装角,φs 为来流角,αs 为迎角,V 0 为飞行器的飞行速度。
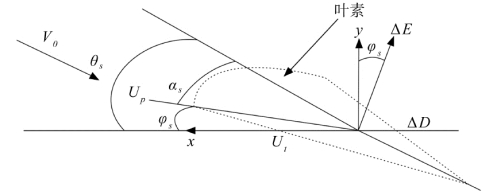
图2.8 叶素受力分析
根据图2.8可知,桨叶叶素的安装角θs、迎角αs 与来流角φs 之间有如下关系:

其中,U p,Ut 为来流在竖直和水平方向上的两个速度分量。和诱导速度v 1 的关系为:
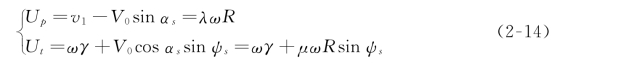
其中,v 1为飞行器以某一速度V 0飞行时旋翼的诱导速度,λ为流入比系数,μ为前进比系数。加载在叶素上的升力E 和阻力D 为:

其中,ΔE称为基元升力,ΔD 称为基元后向力,q为动压,Ct为叶素的基元升力系数,Cd 为叶素的基元后向力系数。
将基元后向力ΔD 和基元升力ΔE 在叶素坐标系上投影,便可得到如下基元阻力ΔF x 和基元拉力ΔF y:
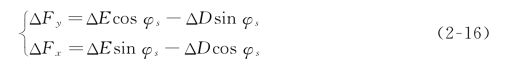
因此根据式(2-16)可得ΔF x ≈-ΔD,ΔF y ≈ΔE。整个旋翼产生的升力F 为:
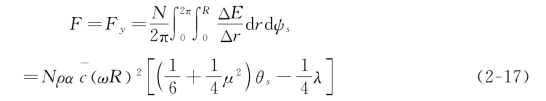
根据上述求取过程可得旋翼的反扭矩Q、阻力D 以及侧倾力矩L,其表达式如下:
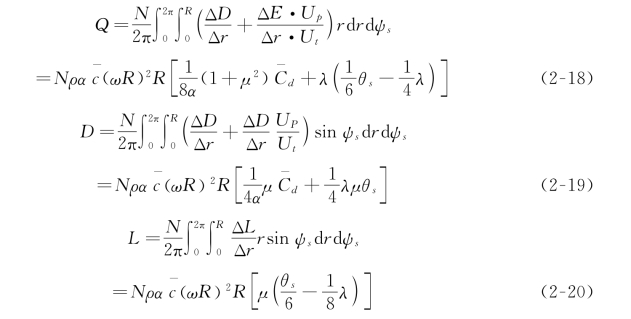
将式(2-17)~(2-20)和式(2-3)对比,可分别得到拉力系数CF,扭矩系数CQ,阻力系数CD,侧倾力矩系数CL 的表达式如下:
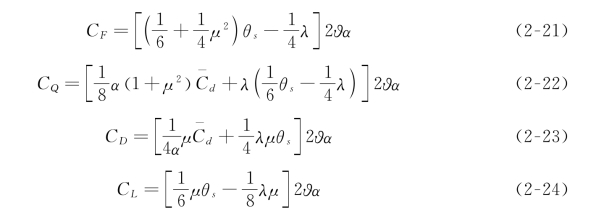
其中,ϑ 为旋翼的实度。
