7.5.2 笛卡尔空间规划方法
如上一节所述,在关节空间中计算出的路径可保证操作臂能够达到中间点和目标点,即使这些路径点是用笛卡尔坐标系来规定的。不过,末端执行器在空间的路径不是直线,而且其路径的复杂程度取决于操作臂特定的运动学特性。在本节讨论的路径生成方法是用笛卡尔位姿关于时间的函数来描述路径形状。此方法可以确定路径点之间的空间路径形状。最常见的路径形状是直线,不过也会使用圆、正弦或其他路径形状。
每个路径点通常由工具坐标系相对于工作台坐标系的期望位姿来确定。在基于笛卡尔空间的路径规划方法中,形成轨迹的样条函数是描述笛卡尔变量的随时间变化的函数。这些路径可直接根据用户指定的路径点进行规划,这些路径点是由{T}相对于{S}来描述的,无需事先进行逆运动学求解。可是,执行笛卡尔规划的计算量很大,因为在运行时必须以实时更新路径速度求出运动学逆解,即在笛卡尔空间生成路径后,最后一步要通过求解逆运动学计算出期望的关节角度。
通常,我们希望能够简单地确定空间路径,使工具的末端在空间做直线运动。显然,如果在一条直线上密集地指定许多分离的中间点,那么不管在中间点之间使用何种光滑函数进行连接,工具末端都走直线。但是,如果能让工具在相隔较远的中间点之间走直线路径,则会更为方便一些。这种定义和执行路径的模式被称作笛卡尔直线运动。使用直线来定义运动是更为一般意义上的笛卡尔运动的子集。在笛卡尔运动中,可以使用笛卡尔变量关于时间的任意函数来定义路径。能完成一般笛卡尔运动的系统,可以执行诸如椭圆或正弦的路径形状。
在规划和生成笛卡尔直线路径时,最好使用带有抛物线拟合的直线样条函数。在每段的直线部分,位置的三个分量都以线性方式发生变化,所以末端执行器会沿着直线路径在空间运动。然而,如果在每个中间点将姿态定义成旋转矩阵,则无法对其分量进行线性插值,因为这样做不一定总能得到有效的旋转矩阵。一个旋转矩阵必须是由正交列向量组成,而在两个有效的矩阵之间对矩阵元素进行插值并不能保证满足这个条件。因此,可以使用另一种姿态的表示方法。

注意,此法与其他笛卡尔-直线-运动规划方法不同,当从一点运动到另一点时,此法不能保证只绕一个“等效轴”旋转。相反,该方法只是能够得到姿态的平衡变换以及可以应用前面介绍过的同样的关节空间轨迹规划的插值方法。(https://www.daowen.com)
另外需要说明的是,姿态的轴角坐标系表示方法不唯一:

一旦对每个中间点选定了χ 的6个值,就可以使用前面介绍的用直线和抛物线组合的样条函数进行路径规划。但是要附加一个约束条件:每个自由度的拟合时间必须是相同的。这样才能保证各自由度形成的复合运动在空间是一条直线。因为各自由度的拟合时间相同,所以在拟合区段的加速度便不相同。因此,在指定拟合区段的时间间隔时,应该使用式(7-107)计算所需要的加速度(而不使用其他方法)。可以通过使用适当的拟合时间以使加速度不超过上限。
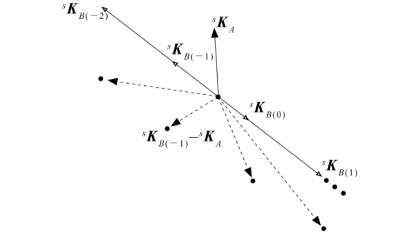
图7.23 轴角坐标系表示法
