4.4 单目视觉系统
顾名思义，单目视觉系统指的是仅仅通过一个摄像头来实现无人机位姿的测量。通过n 个世界点和与之对应的图像坐标点以及摄像机的内部参数来计算摄像机方位的问题称为n 点透视问题，简称为PnP问题。在这里，我们以EPnP算法为例讲解飞行器的位姿估计过程。值得注意的是，内部参数已经在之前的相机标定过程中得以求解。
接下来我将首先讲解一下EPnP算法的原理，尽管这个算法与其他算法一样都已经有现成的函数，但是我们依旧希望能从前人的智慧中窥见一些对未来的展望，这不仅仅是有助于思维的扩展或是对前人贡献的致敬，更是为日后方便读者基于这些理论知识进行创新。
在开始介绍算法之前，出于方便，我们先给出一些符号的定义：
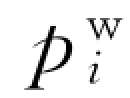：世界坐标系的参考点坐标；
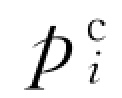：对应于世界坐标系下参考点在相机坐标系下的坐标；
c j：控制点坐标。
假设我们已知n 个参考点的三维坐标以及它们各自对应的图像坐标点。对于一般情况，即n 个参考点不在一个平面，我们可以给定4个不共面的控制点的不同的线性组合来分别表示这n 个参考点；对于n个参考点在同一个平面，我们只需要3个控制点就可以表示这n 个参考点，但是这只是上述情况的特殊情况，其实是包含在原问题里的。
我们用4个给定的控制点来表示参考点坐标，如式（4-30）所示。
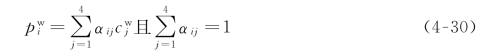
由于世界参考点与控制点的坐标都是已知的，所以αij 也容易求得。
同理，我们可以写出相机坐标系下的关系式（4-31）：
值得注意的是式（4-30）中的αij 与式（4-31）中的是同一个，这个原因也是显然的，这无非是用不同的坐标系来描述同一件事情，因此它们的线性组合系数是不变的。
结合式（4-11）和内参矩阵A 易推得式（4-32）：
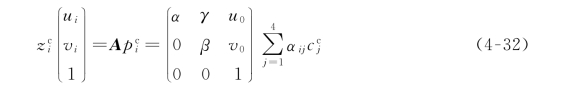
在这里，我们忽略γ 对后续结果的影响，将式（4-32）改写成式（4-33）：
将式（4-34）和式（4-35）写成矩阵形式并简写如下：
其中M 是一个2n×12的矩阵，且容易发现矩阵M 中的系数全是已知量，看上去我们应该直接求解这个线性方程组，这样就可以获取4个控制点在相机坐标系的坐标，然而这样的计算量无疑是很大的，在这里我们采用了巧妙的方法求解该问题。众所周知，M T Mx＝0与Mx＝0同解，我们只需求解M T M 特征值为0的特征向量V i，显然这是不难求得的，不妨设M T M 特征值为0的特征向量共有N 个，进而可以求出：
当N ＝2时，我们有x＝β1V 1＋β2V 2，因此我们的距离约束变为下式：
将式（4-41）展开后β1，β2 混合在了一起，这不利于我们的求解。这里我们采用线性化的技巧解决这个问题，令β11＝β1·β1，β12＝β1·β2，β22＝β2·β2，由于4个控制点意味着有6个距离约束关系，结合式（4-41）写成线性方程形式：
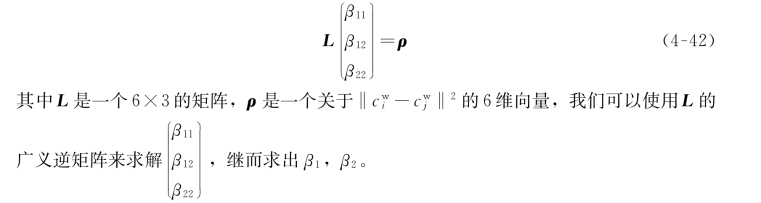
当N ＝3时，这与N ＝2时是类似的，我们也可以求出一个线性方程：
当N＝4时，我们只有4个β未知，有6个约束条件，理论上是可以求解的，但是实际上由于线性化的步骤使得我们实际上产生了10个未知量βαb。因此我们采取再线性化的措施，并依此求出β1，β2，β3，β4。
尽管我们已经将4种N 取值的情况下β系数算出来了，但是我们并不能保证β的精确性，因此在这里我们使用高斯牛顿迭代法来最小化下述目标函数来微调β 系数：
结合式（4-7）可以发现式子本身有9个未知外参数，其中蕴含着5个约束分别是旋转向量相互垂直，旋转向量模长为1。因此我们只需要已知4个世界参考点坐标和与之对应的图像坐标就可以求解出外参矩阵，获取机载相机的位置和姿态。