7.2.1 连杆坐标系的描述和规定
操作臂可以看成由一系列刚体通过关节连接而成的一个运动链，我们将这些刚体称为连杆。
三维空间中的任意两个轴之间的距离均为一个确定值，两个轴之间的距离即为两轴之间公垂线的长度。如图7.4所示，关节轴i－1和关节轴i之间公垂线的长度为αi－1，αi－1 即为连杆长度。用来定义两关节轴相对位置的第二个参数为连杆转角。假设作一个平面，并使该平面与两关节轴之间的公垂线垂直，然后把关节轴i－1和i投影到该平面上，在平面内轴i－1按照右手定则绕αi－1 转向轴i，测量两轴线之间的夹角，用转角αi－1 定义连杆i－1的扭转角。图7.4中，αi－1 表示关节轴i－1和i之间的夹角。当两个关节轴线相交时，两轴线之间的夹角可以在两者所在的平面中测量，但是αi－1 没有意义。在这种特殊情况下，αi－1 的大小和符号可以任意选取。
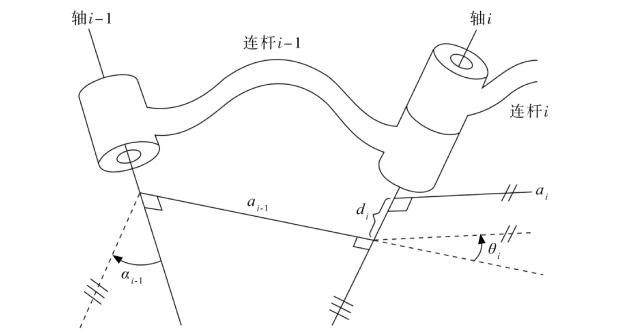
图7.4 操作臂连杆连接
为了描述每个连杆与相邻连杆之间的相对位置关系，需要在每个连杆上定义一个固连坐标系。根据固连坐标系所在连杆的编号对固连坐标系命名，因此，固连在连杆i上的固连坐标系称为坐标系｛i｝。
1）连杆链中的中间连杆。
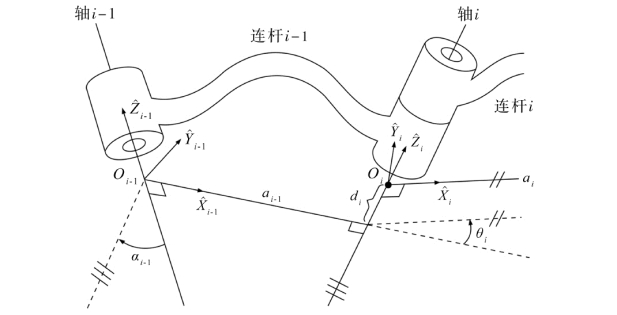
图7.5 固连于连杆i上的连杆坐标系｛i｝
2）连杆链中的首尾连杆。
固连于机器人基座（即连杆0）上的坐标系为坐标系｛0｝。这个坐标系是一个固定不动的坐标系，因此在研究操作臂运动学问题时，可以把该坐标系作为参考坐标系。可以在这个参考坐标系中描述操作臂所有其他连杆坐标系的位置。
参考坐标系｛0｝可以任意设定，但是为了使问题简化，通常设定Z^0 轴沿关节轴1的方向，并且当关节变量1为0时，设定参考坐标系｛0｝与坐标系｛1｝重合。按照这个规定，总有α0＝0.0和α0＝0.0。另外，当关节1为转动关节时，d 1＝0.0；当关节1为移动关节时，θ1＝0.0。
4）建立连杆坐标系的步骤。
对于一个新机构，可以按照下面的步骤正确地建立连杆坐标系。
（1）找出各关节轴，并标出（或画出）这些轴线的延长线。在下面的步骤2至步骤5中，仅考虑两个相邻的轴线（关节轴i和i＋1）。
（2）找出关节轴i和i＋1之间的公垂线或关节轴i和i＋1的交点，以关节轴i和i＋1的交点或公垂线与关节轴i的交点作为连杆坐标系｛i｝的原点。
