3.4.1　加速度计积分

3.4.1　加速度计积分

加速度是一个对象速度的变化速率，速度是一个对象位置的变化速率。换句话说，速度是位置的导数，加速度是速度的导数，因此有如下公式：

积分和导数相反。如果一个物体的加速度已知，那么我们能够利用二重积分获得物体的位置。假设初始条件为0，那么有如下公式：

一个理解这个公式的方法是将积分定义成曲线下面包围的区域，积分运算结果是极小区域的总和，区域的宽度趋近于0。换句话说，积分的和表示了一个物理变量的大小（速度）。

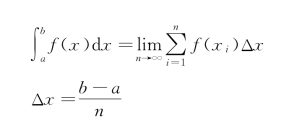
利用曲线下方区域的概念，我们能得出一个结论：对一个信号采样，得到该信号大小的瞬时值，这样就能够在两次采样之间得到一个小的区域。为了获得连贯的值，采样时间必须相同。采样时间代表这块区域的宽，同时采样得到的值代表区域的高。

设加速度函数为x（t），则速度函数y（t）与它的关系如式（3-6）所示，x（t）拉氏变换函数为x（s），y（t）拉氏变换为y（s），则将式（3-6）进行拉氏变换后如式（3-7）所示：

所以加速度积分的模型如图（3.12）所示，图中x（s）为加速度的S域函数，y（s）为积分后的速度S 域函数。

由1/s的Z 变换为1/（1－1/z）可以将式（3-7）转换到Z 域，如下式：

由上式可以进一步得到加速度和积分后的速度的差分方程关系：

其中y（k）是速度的第k个采样点，y（k－1）是速度的第k－1个采样点，x（k）是加速度的第k 个采样点。

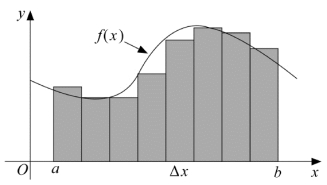
图3.12　加速度积分

积分会对误差积累，随着时间的推移积分出的误差就会越来越明显。因此实际测得的加速度零点可能偏上或者偏下，这样就会导致积分出的速度整体以一定的斜率向上或者向下漂移，需要对计算出的速度进行误差补偿。