7.5.1 关节空间规划方法
本节将研究以关节角的函数来描述轨迹(在空间和时间两个维度)的生成方法。
每个路径点通常是用工具坐标系{T}相对于工作台坐标系{S}的期望位姿来确定的。应用逆运动学理论,将中间点“转换”成一组期望的关节角。这样,就得到了经过各中间点并终止于目标点的n 个关节的光滑函数。对于每个关节而言,由于各路径段所需要的时间是相同的,因此所有的关节将同时到达各中间点,从而得到{T}在每个中间点上的期望的笛卡尔位置。尽管对每个关节指定了相同的时间间隔,但对于某个特定的关节而言,其期望的关节角函数与其他关节函数无关。
因此,应用关节空间规划方法可以获得各中间点的期望位姿。尽管各中间点之间的路径在关节空间中的描述非常简单,但在笛卡尔坐标空间中的描述却很复杂。一般情况下,运用关节空间规划方法便于计算,并且由于关节空间与笛卡尔坐标空间之间并不存在连续的对应关系,不会发生机构的奇异性问题。
1)三次多项式。
下面考虑在一定时间内将工具从初始位置移动到目标位置的问题。应用逆运动学可以解出对应于目标位姿的各个关节角。操作臂的初始位置是已知的,并用一组关节角进行描述。现在需要确定每个关节的运动函数,其在t 0时刻的值为该关节的初始位置,在t f 时刻的值为该关节的期望目标位置。如图7.17所示,有多种光滑函数θ(t)均可用于对关节角进行插值。
为了获得一条确定的光滑运动曲线,显然至少需要对θ(t)施加四个约束条件。通过选择初始值和最终值可得到对函数值的两个约束条件:

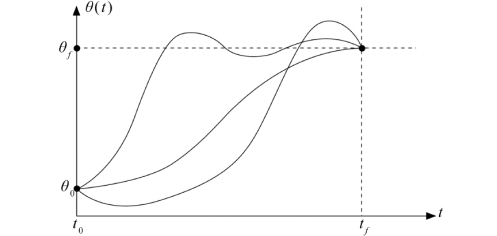
图7.17 某一关节的几种可能的路径曲线
另外两个约束条件需要保证关节速度函数连续,即在初始时刻和终止时刻关节速度为零:

三次多项式才能满足这四个约束条件[一个三次多项式有4个系数,所以它能够满足由式(7-90)和式(7-91)给出的约束条件]。这些约束条件确定了一个唯一的三次多项式。该三次多项式具有如下形式:
![]()
所以对应于该路径的关节速度和加速度显然有:

把这四个期望的约束条件代入式(7-92)和式(7-93)可以得到含有四个未知量的四个方程:
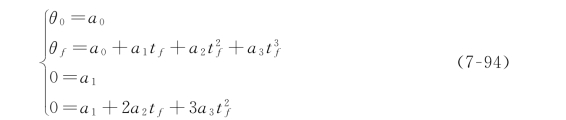
解出方程中的αi,可以得到:
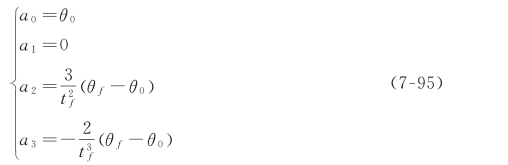
应用式(7-95)可以求出从任何起始关节角位置到期望终止位置的三次多项式。但是该解仅适用于起始关节角速度与终止关节角速度均为零的情况。
2)具有中间点的路径的三次多项式。
到目前为止,已经讨论了用期望的时间间隔和最终目标点描述的运动。一般而言,操作臂希望确定包含中间点的路径。如果操作臂能够停留在每个中间点,那么可以使用上述的三次多项式求解。
通常,操作臂需要连续经过每个中间点,所以应该归纳出一种能够使三次多项式满足路径约束条件的方法。
与单目标点的情形类似,每个中间点通常是用工具坐标系相对于工作台坐标系的期望位姿来确定的。应用逆运动学把每个中间点“转换”成一组期望的关节角。然后,考虑对每个关节求出平滑连接每个中间点的三次多项式。
如果已知各关节在中间点的期望速度,那么就可以像前面一样构造出三次多项式。但是,这时在每个终止点的速度约束条件不再为零,而是已知的速度。于是,式(7-91)的约束条件变成:

描述这个一般三次多项式的四个方程为:
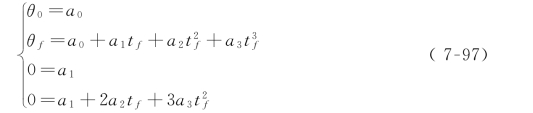
求解方程组中的αi,可以得到:
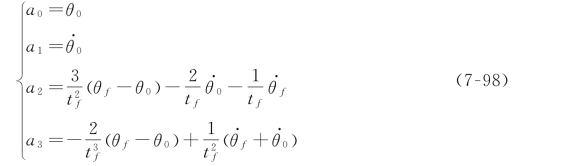
应用式(7-98),可求出符合任何起始和终止位置以及任何起始和终止速度的三次多项式。
如果在每个中间点处均有期望的关节速度,那么可以简单地将式(7-98)应用到每个曲线段来求出所需的三次多项式。确定中间点处的期望关节速度可以使用以下几种方法。
(1)根据工具坐标系的笛卡尔线速度和角速度确定每个中间点的瞬时期望速度。
(2)在笛卡尔空间或关节空间使用适当的启发式方法,系统自动选取中间点的速度。
(3)采用使中间点处的加速度连续的方法,系统自动选取中间点的速度。
第(1)种方法,利用在中间点上计算出的操作臂的雅可比逆矩阵,把中间点的笛卡尔期望速度“映射”为期望的关节速度。如果操作臂在某个特定的中间点上处于奇异位置,则用户将无法在该点处任意指定速度。对于一个路径生成算法而言,其用处之一就是满足用户指定的期望速度。然而,总是要求用户指定速度也是一个负担。因此,一个方便的路径规划系统还应包括方法(2)或(3)(或二者都有)。
第(2)种方法,系统使用一些启发式方法来自动地选择合理的中间点速度。图7.18所示为由中间点确定的某一关节θ 的路径的方法。
在图7.18中,已经合理选取了各中间点上的关节速度,并用短直线来表示,这些短直线即为曲线在每个中间点处的切线。这种选取结果是通过使用了概念和计算方法都很简单的启发式方法而得到的。假设用直线段把中间点连接起来。如果这些直线的斜率在中间点处改变符号,则把速度选定为零;如果这些直线的斜率没有改变符号,则选取两斜率的平均值作为该点的速度。这样,系统可以只根据规定的期望中间点,来选取每个中间点的速度。
第(3)种方法,系统根据中间点处的加速度为连续的原则选取各点的速度。为此,需要一种新的方法。在这种样条曲线中设置一组数据,在两条样条曲线的连接点处,用速度和加速度均为连续的约束条件替换两个速度约束条件。
 (https://www.daowen.com)
(https://www.daowen.com)
图7.18 有切线标记的点为期望速度的中间点
3)高阶多项式。
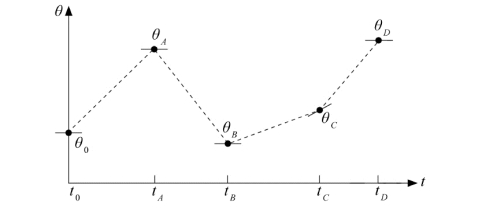
有时用高阶多项式作为路径段。例如,如果要确定路径段起始点和终止点的位置、速度和加速度,则需要用一个五次多项式进行插值:
![]()
其约束条件为:这些约束条件确定了一个具有6个方程6个未知数的线性方程组,其解为:
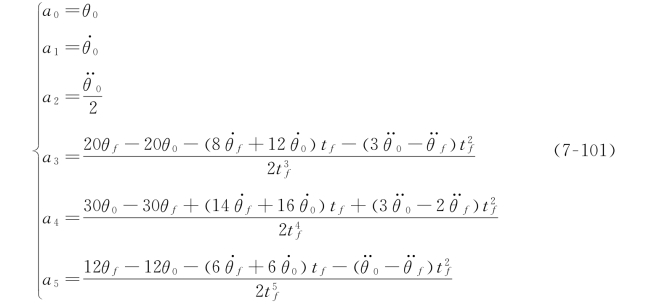
对于一个途经多个给定数据点的轨迹来说,可用多种算法来求解描述该轨迹的光滑函数(多项式或其他函数)。
4)与抛物线拟合的线性函数。
另外一种可选的路径形状是直线。即简单地从当前的位置关节进行线性插值,直到终止位置,如图7.19所示。请记住,尽管在该方法中各关节的运动是线性的,但是末端执行器在空间的运动轨迹一般不是直线。
然而,直接进行线性插值将导致在起始点和终止点的关节运动速度不连续。为了生成一条位置和速度都连续的平滑运动轨迹,先用线性函数,但需在每个路径点增加一段抛物线拟合区域。
在运动轨迹的拟合区段,将使用恒定的加速度平滑地改变速度。图7.20所示为使用这种方法构造的简单路径。直线函数和两个抛物线函数组合成一条完整的位置与速度均连续的路径。
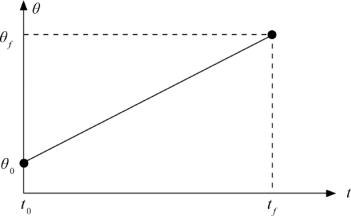
图7.19 线性插值要求加速度无限大
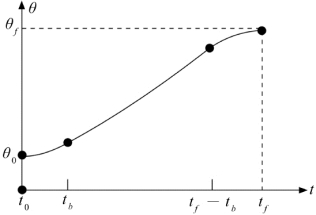
图7.20 带有抛物线拟合的直线段
为了构造这样的路径段,假设两端的抛物线拟合区段具有相同的持续时间,因此在这两个拟合区段中采用相同的恒定加速度(符号相反)。如图7.21所示,这里存在有多个解,但是每个结果都对称于时间中点t h 和位置中点θh。由于拟合区段终点的速度必须等于直线段的速度,所以有:
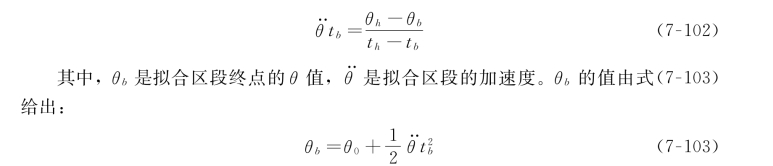
联立式(7-102)和式(7-103),且t=2t h,可以得到:

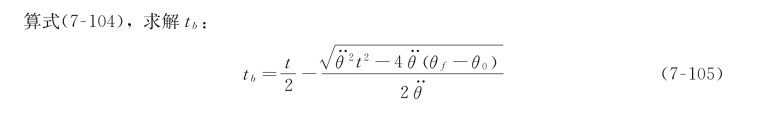
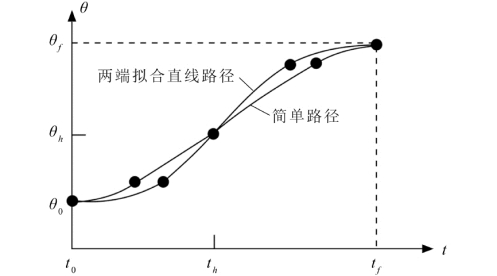
图7.21 带有抛物线拟合的直线段
在拟合区段使用的加速度约束条件为
![]()
当式(7-106)中等号成立时,直线部分的长度缩减为零,整个路径由两个拟合区段组成,且衔接处的斜率相等。如果加速度的取值越来越大,则拟合区段的长度将随之越来越短。当处于极限状态时,即加速度无穷大,路径又恢复到简单的线性插值情况。
5)具有中间点的路径与抛物线拟合的线性函数。
现在讨论带有抛物线拟合的直线路径,路径上指定了任意数量的中间点。图7.22所示为某个关节θ 在关节空间的一组中间点,中间点之间使用线性函数相连,而各中间点附近使用抛物线拟合。

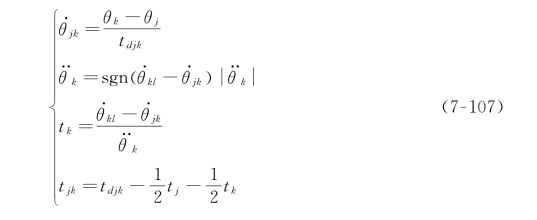
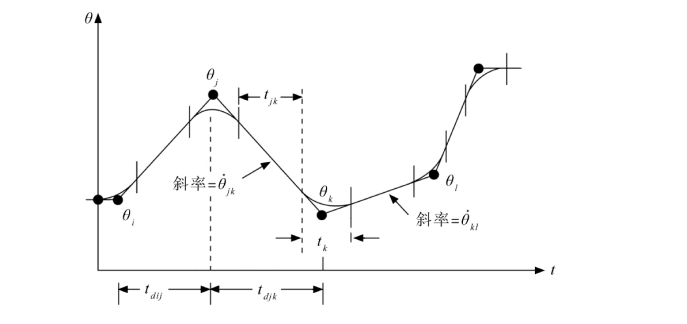
图7.22 多段带有拟合区段的直线路径
但是,对于第一个路径段和最后一个路径段的处理稍有不同,因为路径末端的整个拟合区段都必须计入到总路径段的时间间隔中。
对于第一个路径段,令线性区段速度的两个速度表达式相等来求解t 1:

同样,对于最后一个路径段(连接点n-1到n),有:

可求出:
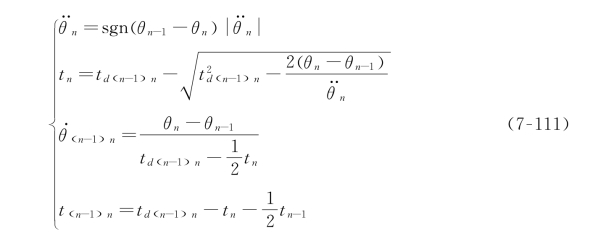
式(7-107)~式(7-111)可用来求出多段轨迹中各个拟合区段的时间和速度,通常用户只需给定中间点以及各个路径段的持续时间。在这种情况下,系统使用各个开关的默认加速度值。有时,为了方便用户,系统还可以按照默认的速度来计算持续时间。对于各个拟合区段,加速度值必须取得足够大,以便在下一个拟合区段开始之前有足够的时间进入直线区段。
