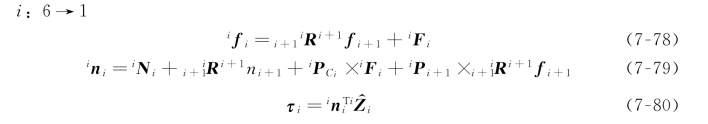7.4.2 牛顿-欧拉迭代动力学方程
1）计算速度和加速度的向外迭代法。
为了计算作用在连杆上的惯性力，需要计算操作臂每个连杆在某一时刻的角速度、线加速度和角加速度。可应用迭代方法完成这些计算。首先对连杆1进行计算，接着计算下一个连杆，这样一直向外迭代到连杆n。
在第7.3节中已经讨论了角速度在连杆之间的“传递”问题，且有（对于第i＋1个关节的旋转运动）：
由式（7-58）可以得到连杆之间角加速度变换的方程：
当第i＋1个关节是移动关节时，式（7-60）可简化为：
利用式（7-55）可以得到每个连杆坐标系原点的线加速度：
当第i＋1个关节是移动关节时，根据式（7-53），式（7-62）可简化为：
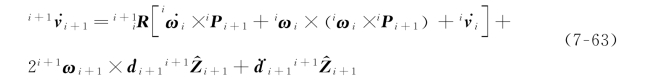
同理，应用式（7-55）可以得到每个连杆重心的线加速度：
假定坐标系｛Ci｝固连于连杆i上，坐标系原点位于连杆重心，且各坐标轴方位与原连杆坐标系｛i｝方位相同。由于式（7-59）与关节的运动无关，因此无论是旋转关节还是移动关节，式（7-59）对于第i＋1个连杆来说都是有效的。
注意，第1个连杆的方程非常简单，因为0ω0＝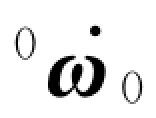
＝0。
2）作用在连杆上的力和力矩。
计算出每个连杆重心的线加速度和角加速度之后，运用牛顿-欧拉公式便可以计算出作用在连杆重心上的惯性力和力矩：
其中，坐标系｛Ci｝的原点位于连杆重心，各坐标轴方位与原连杆坐标系｛i｝方位相同。
3）计算力和力矩的向内迭代法。
计算出作用在每个连杆上的力和力矩之后，需要计算关节力矩，它们是实际施加在连杆上的力和力矩。
根据典型连杆在无重力状态下的受力图（见图7.16）列出力平衡方程和力矩平衡方程。每个连杆都受到相邻连杆的作用力和力矩以及附加的惯性力和力矩。
将所有作用在连杆i上的力相加，得到力平衡方程：
将所有作用在重心上的力矩相加，并且令它们的和为零，得到力矩平衡方程：
利用式（7-66）以及附加旋转矩阵的办法，式（7-67）可写成：
最后，重新排列力和力矩方程，形成相邻连杆从高序号向低序号排列的迭代关系：
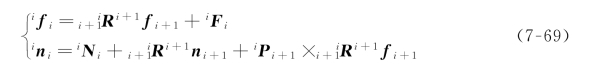
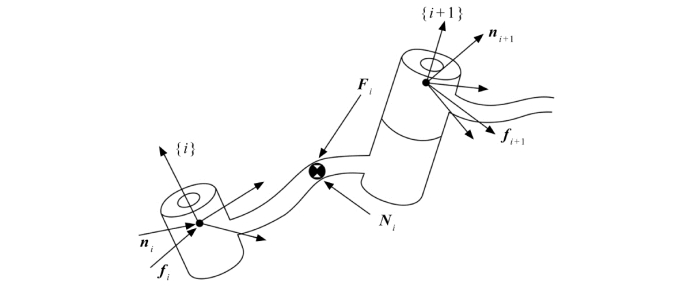
图7.16 无重力状态受力图
应用这些方程对连杆依次求解，从连杆n 开始向内迭代一直到机器人基座。这些向内迭代求力的方法与第7.3节中介绍的静力学迭代方法相似，只是惯性力和力矩是作用在每个连杆上的。
在静力学中，可通过计算一个连杆施加于相邻连杆的力矩在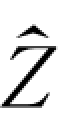
方向的分量求得关节力矩：
对于移动关节，有：
其中，τ 表示线性驱动力。
注意，对一个在自由空间中运动的机器人来说，N ＋1 f N ＋1 和N ＋1n N ＋1 等于零，因此应用这些方程首先计算连杆n 时是很简单的。如果机器人与环境接触，N ＋1f N ＋1和N ＋1 n N ＋1 不为零，力平衡方程中就包含了接触力和力矩。
4）牛顿-欧拉迭代动力学算法。
由关节运动计算关节力矩的完整算法由两部分组成。第一部分是对每个连杆应用牛顿-欧拉方程，从连杆1到连杆n 向外迭代计算连杆的速度和加速度。第二部分是从连杆n 到连杆1向内迭代计算连杆间的相互作用力和力矩以及关节驱动力矩。对于转动关节来说，这个算法归纳如下：
外推：
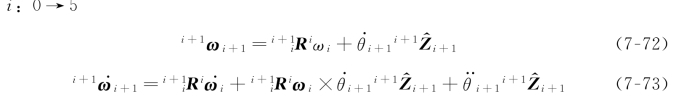
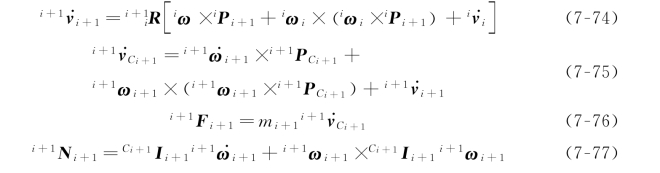
内推：
