5.3.3 基于EKF的SLAM 研究
1）卡尔曼滤波器理论介绍。
卡尔曼滤波（Kalman filtering），是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作滤波过程。
图5.8描述了卡尔曼滤波器估计的一般方案。图中系统有一个控制信号和作为输入的系统误差源。测量装置能够测量带有误差的某些系统状态。卡尔曼滤波器是基于系统的知识和测量装置，产生系统状态最优估计的一个数学机制，是对系统噪声、测量误差和动态模型不确定性的描述。因此，卡尔曼滤波器以最优的方式，融合了测量传感器信号和系统知识。其最优性依赖于评估特性指标所选的判据和假设。在卡尔曼滤波器理论中，系统被假定为线性并具有高斯白噪声。
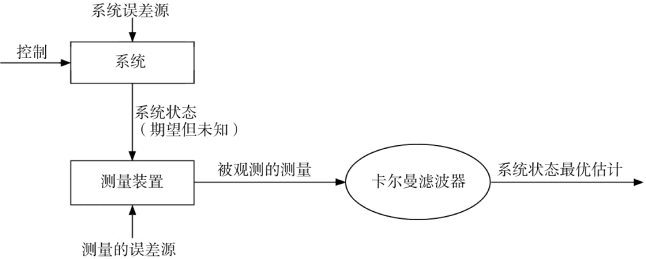
图5.8 卡尔曼滤波框架图
可以将卡尔曼滤波理解为一种比平均滤波更加优秀、更加动态的算法。
卡尔曼滤波器也有自己的约束条件，所以在使用卡尔曼滤波器之前，系统务必满足的条件：
①x k ＝A·x k－1＋B·u k ＋w k－1
其中，x k 是一个线性随机方程，w k－1 是一个过程噪声（高斯），A，B 是系统固有参数；
②z k ＝H·x k ＋v k
其中，z k 也是线性的，v k 是测量噪声（高斯），H 是测量系统固有参数。
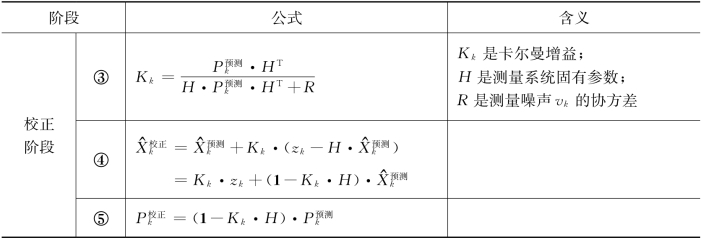
卡尔曼滤波过程可以分为两步，预测阶段和校正阶段，不断地融合本体传感器和外式传感器的数据从而得到更加精准的数据。卡尔曼滤波器的具体公式如表5-1。
表5-1 卡尔曼滤波器计算公式
续表
2）卡尔曼滤波器定位。
卡尔曼滤波定位算法是马尔可夫定位的一个特殊情况。卡尔曼滤波器不使用任何密度函数，而是使用高斯函数代表机器人的信任度、运动模型和测量模型。因为高斯函数简单地由它的均值和协方差来定义。在预测和测量阶段这两个参数被更新。于是产生了和马尔可夫定位算法相比更为有效的算法，然而卡尔曼滤波器所做的假设限制了初始信任度以及高斯函数的选择，这意味着我们必须以一定的近似值知道机器人的初始位置。否则，如果机器人丢失，它就不能恢复到初始位置。这与马尔可夫定位正好相反。所以卡尔曼滤波器着重于位置跟踪问题，而不是全局定位问题。
3）扩展卡尔曼滤波。
对绝大多数移动机器人应用系统是非线性的。在这种情况下，通常在线性化系统之后应用卡尔曼滤波器。卡尔曼滤波器扩充到非线性系统，称之为扩展卡尔曼滤波器。
扩展卡尔曼滤波器中，假定系统是线性的，整个机器人的方位、里程计误差模型以及测量误差模型都受高斯白噪声的影响。
高斯分布由一次和二次矩（即均值和协方差）表示，当机器人的方位是一个向量时，分布是一个多变量向量，用均值向量和协方差矩阵表示。卡尔曼滤波过程分为预测和测量两步骤，依据的理论是全概率定理和贝叶斯定理。在预测和测量更新期间，只更新均值和协方差。所以卡尔曼滤波器是基于4个方程来进行更新的：2个用来预测更新均值和协方差，另外2个用来校正更新。
应用全概率定理，x 1 和x 2 相互独立，服从正态分布：x 1 ～N（μ1，σ21），x 2 ～N（μ2，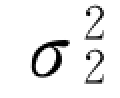
），y＝f（x 1，x 2），目的是求y 的分布状况。
若f 是线性函数，y＝A x 1＋B x 2，那么其均值、方差和协方差表达式如下：
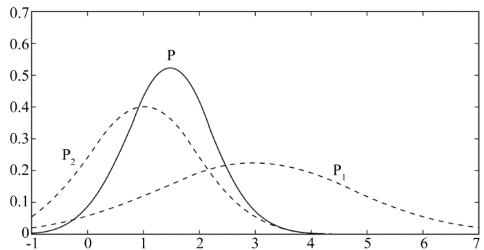
图5.9 正态分布图
由上述公式能清楚地看到，生成的方差σ2 既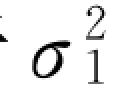小于
也小于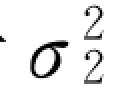
。因此，可通过机器人信任度和外感受式传感器测量的组合来降低位置估计的不确定性。