5.5.2 三维环境下使路径平滑的人工势场法
1)三维环境下障碍物点的提取方法。
本节所用算法将一个个的障碍点作为产生斥力场的源,生成的三维空间地图是由众多点构成的三维空间连续曲面,故可将这些分布在连续障碍物表面的点作为障碍点进行提取,提取方法如图5.14所示。
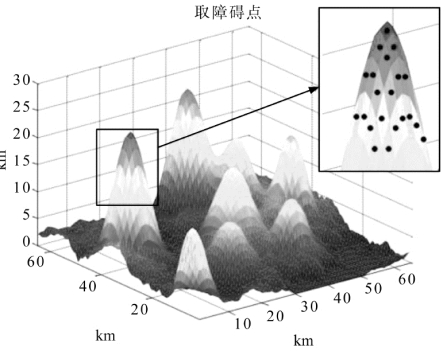
图5.14 取障碍点示意图
2)改进的人工势场法。
单独使用A* 算法产生的路径由一系列直线段连接构成,路径的一阶导数在连接点处均不连续,平滑性和跟踪性较差,考虑到人工势场法结构简单,计算量小,在平滑路径和动态避障方面应用广泛,选择对传统人工势场法进行改进并与改进的A* 算法相结合。
针对传统人工势场法存在的问题,对斥力函数进行了改进。此外,为了克服传统人工势场法可能陷入局部最优解的问题,在平滑算法时增设多目标点,具体操作如下:
假设使用A*算法得到的初步路径为S→A →B→…→N →T,其中S为起点,T为终点。当飞行机器人处于点A 时将下一点B 作为引力点,三维地图模型中各个障碍点作为斥力点,利用人工势场法对A 到B 的路径进行平滑,以此类推。
引力势场和引力函数仍然采用原方式表示,如式(5-13)和式(5-14)所示。

其中,k表示引力常量,d g 表示旋翼式飞行机器人当前位置到目标或下一引力点的距离。
针对目标不可达的问题对斥力函数进行了改进,在考虑斥力场的时候要计算飞行机器人与目标点之间的距离。新的斥力场函数如式(5-15)所示。
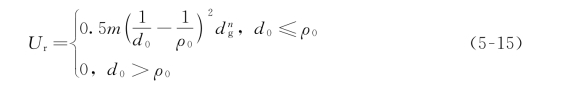 (https://www.daowen.com)
(https://www.daowen.com)
其中,m 表示斥力常量,d 0 表示旋翼式飞行机器人从当前位置到障碍物的距离,d g 表示飞行机器人从当前位置到目标点的距离,ρ0 表示障碍物的影响距离。
相应的斥力大小以式(5-16)~式(5-18)形式表示:
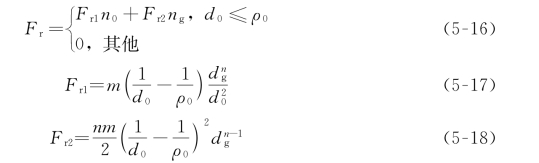
如图5.15所示,力在三维空间中先分解为一个沿z轴的分力和一个x O y 平面的分力,夹角为θ1,再将F xy 分解为沿x 轴和沿y 轴的分力。
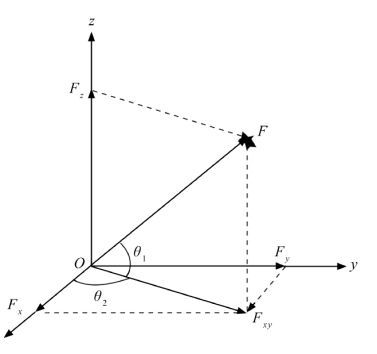
图5.15 三维空间中力的分解示意图
当飞行机器人第j步路径点X j =(x j,y j,z j)时,机器人受到前向目标点引力和障碍物的斥力。由式(5-19)~(5-21)得到目标点所受引力在三个坐标轴的分力,由式(5-22)~(5-24)得到目标点所受斥力在三个坐标轴的分力大小。
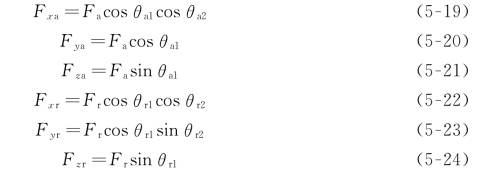
其中,θa1为所在位置X j 与引力点的连线与x Oy平面的夹角,θa2为所在位置X j 在x Oy平面的投影点与引力点的连线与x 轴的夹角,θr1为所在位置X j 与障碍物的连线与x Oy平面的夹角,θr2 为所在位置X j 在x Oy 平面的投影点与障碍物的连线与x 轴的夹角。
将引力和斥力分别在三个坐标轴上进行合成后,再将三个分力再次合成后得到所受的合力大小,如式(5-25)、式(5-26)所示
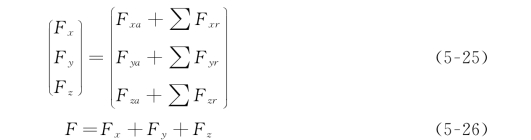
合力决定了飞行机器人下一刻的运动方向,可通过修改m 的值调节斥力大小,通过改变n 的值使得路径达到最优平滑效果。当到达最后一个引力点时,即引力为0时结束路径平滑过程,由此得到一条光滑的无碰撞路径。
