7.6.1 单关节的建模和控制
许多工业机器人常用的驱动器是直流（DC）力矩电机。电机中不转动的部分（定子）由机座、轴承、永久磁铁或电磁铁组成。定子中的磁极产生一个穿过电机转动部件（转子）的磁场。转子由电机轴和线圈绕组组成，电流通过线圈绕组产生电机转动的能量。电流经与换向器接触的电刷流入线圈绕组。换向器与变化的线圈绕组（也称为电枢）以某种方式相连接便产生指定方向的转矩。当电流通过线圈绕组时电机会产生转矩的物理现象可以表示为：
这里电荷q以速度v通过磁场强度为B 的区域时将产生一个力F。电荷为通过线圈绕组的电子，磁场由定子磁极产生。一般来说，电机产生转矩的能力用电机转矩常数表示，电枢电流与输出转矩的关系可表示为：
当电机转动时，则成为一个发电机，在电枢上产生一个电压。电机的另一个常数——反电势常数，表示给定转速时产生的电压：
一般来讲，换向器实际上是一个开关，它使电流通过变化的线圈绕组产生转矩，并产生一定的转矩波动。尽管有时这个影响很重要，但通常这种影响可忽略不计（在任何情况下，建立这个模型都是相当困难的，即使建立了模型，误差补偿也是相当困难的）。
1）电机电枢感抗。
图7.24所示为电枢电路。主要的构成部分是电源电压V、电枢绕组的感抗L、电枢绕组的电阻R 以及产生的反电势E。这个电路由如下一阶微分方程描述：
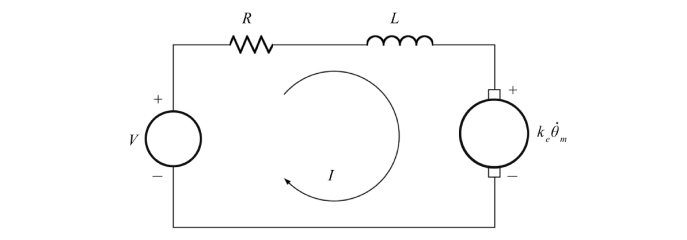
图7.24 直流力矩电机的电枢电路
一般用电机驱动器控制电机的转矩（而不是速度）。驱动电流通过检测电枢电流不断调节电源电压V 以使通过电枢的电流为期望电流I。在电流驱动系统中，由电机感抗L和电源电压的上限V 控制电枢电流变化的速率。实际上相当于在工作电流和输出转矩之间存在一个低通滤波器。
为简化起见，首先假设电机的感抗可以忽略。当闭环控制系统的固有频率远低于由于感抗引起的电流驱动器中隐含的低通滤波器的截止频率时，这个假设便是合理的。这个假设和转矩波动假设一样都可以忽略不计，这表明电机转矩可以直接控制。虽然存在某个比例因子（例如k m），但仍可以将驱动器视为可以直接控制的纯力矩源。
2）有效惯量。
图7.25所示为通过齿轮减速器与惯性负载相连的直流力矩电机转子的力学模型。式（7-120）表示作用于转子的扭矩τm 是电枢电流I的函数。传动比（η）可提高驱动负载的力矩、降低负载的转速，由式（7-123）表示：
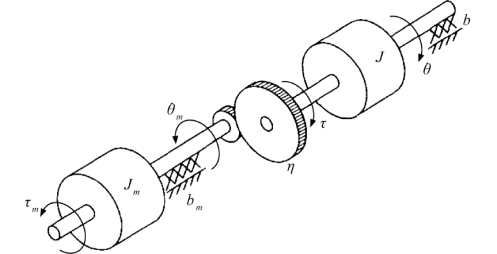
图7.25 通过齿轮减速器与惯性负载相连的直流力矩电机转子的力学模型
其中，η ＞1。按照转子力矩写出系统的力矩平衡方程如下：
其中，J m 和J 分别为电机转子惯量和负载惯量，bm 和b分别为电机转子轴承和负载轴承的黏滞摩擦系数。由式（7-123），将式（7-124）按照电机变量改写为：
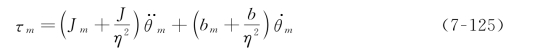
或根据负载变量改写为：
其中，J＋η2J m 为减速器输出端（连杆侧）的有效惯量，b＋η2bm 为有效阻尼。注意，在大传动比（即η ≫1）的情况下，电机转子惯量是有效组合惯量中的主要部分。正是这个原因我们才能够假设有效惯量是一个常数。由第7.5节可知，机构关节的惯量J实际上是随着机构位形和负载变化的。然而在大传动比的机器人中，这种变化的比例小于直接驱动操作臂（即η＝1）。为确保机器人连杆的运动永远不为欠阻尼，J值应为取值范围内的最大值，即J max。这样可以保证系统在任何情况下均为临界阻尼或者过阻尼。
3）单关节控制。
概括来说，我们建立了三个主要假设。
（1）电机的感抗L 可以忽略。
（2）考虑大传动比的情况，将有效惯量视为一个常数，即J max＋η2 J m。
（3）结构柔性可以忽略，最低结构共振频率ωres 用于设定伺服增益的情况除外。
应用这些假设，可以用下式给出的分解运动对一个单关节操作臂进行控制。
系统的闭环动力学方程为：
式中的增益取：
