8.2.2 带臂旋翼无人机的动力学模型
系统动力学模型由飞行平台和机械臂组成，完整的动力学需要考虑二者之间的耦合作用，并对其整体进行建模分析。由于带臂旋翼飞行器系统在实际作业中机械臂大部分时间（作业前和作业后）处于静态状态，只有在对目标进行作业时才是动态的，且机械臂运动速度缓慢，对系统而言可以看成是变化的静态状态。所以可以对系统静态情况下的动力学进行建模分析。
系统在静态情况下与普通飞行平台动力学建模的主要区别在于其重心是可变的，并且一般不在飞行平台的几何中心点。系统重心不在几何中心时的示意图如图8.3所示。
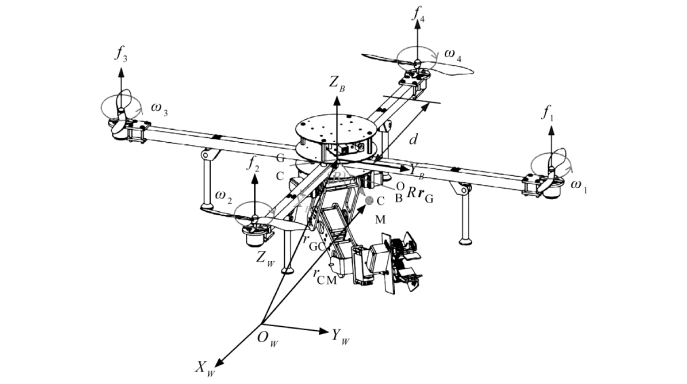
图8.3 系统重心偏移结构示意图
在图8.3中，重心偏移向量r G ＝（x G，y G，z G）T 是系统重心（center of gravity，CM）在坐标系｛B｝中的向量，r CM 是其在坐标系｛W｝的位置向量。几何中心（geometric center，GC）是飞行平台的几何中心，与坐标系｛B｝的原点重合，r GC 是GC在坐标系｛W｝中的位置向量。
目前动力学建模主要方法有：牛顿-欧拉方程法和拉格朗日动力学方程法。使用拉格朗日动力学方程法时，需要对系统各部分的动能和势能进行计算，得出的动力学方程的形式较为复杂。
系统的牛顿方程和欧拉方程为：
四旋翼飞行器有4个电机，运转方式如图8.3所示。其中1号电机和3号电机逆时针运转，2号和4号电机顺时针运转，4个电机都产生向上的升力和与电机旋转方向相反的反作用力。
电机升力f i 和反作用力g i 的计算公式为：
其中，ωi 表示第i个电机转速，对于特定空气与桨叶b和k都是常数，其大小与空气密度、阻力系数、螺旋桨几何参数等有关。飞行平台的动力完全由4个电机提供，分析系统受力可知外力F 和外部转矩M 为：
u i 为：
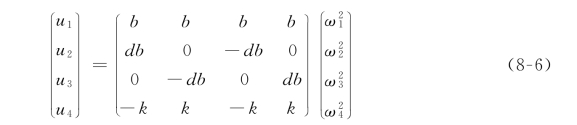
其中，b是升力常数，d 是电机升力力臂长度。
联立式（8-4）～（8-6）可得旋翼飞行机械臂系统动力学方程为：
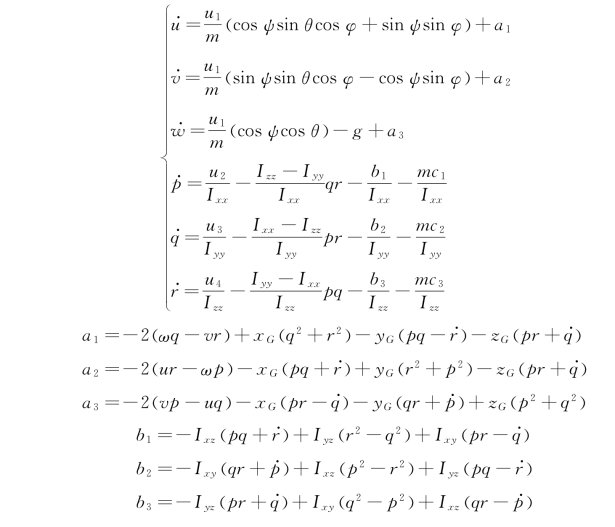
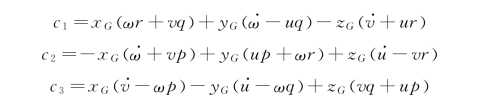
其中，α1，α2，α3，b 1，b 2，b 3 是由系统重心不与几何中心点重合而产生的额外作用项，其可以由系统状态和重心位置坐标进行计算。